Inference for Regression

November 11, 2025

From Fitting to Inference

We’ve learned how to:

• Fit a least squares line \(\widehat{y} = b_0 + b_1x\)
• Interpret \(b_1\) (slope) and \(b_0\) (intercept)
• Compute residuals and \(R^2\)

Now we’ll ask:

How certain are we about this line?
Would the slope change if we took another sample?
How variable are our predictions?

Regression

Two Questions of Uncertainty

1. Model uncertainty:
   How much could \(b_1\) vary across samples?

2. Prediction uncertainty:
   How much could \(\widehat{y}\) vary for new individuals?

Inference Questions

• Slope uncertainty: How much could \(b_1\) change if we resampled?
• Prediction uncertainty: How variable is \(\widehat{y}\) for a new \(x\)?
• Confidence intervals of model coefficients and slope.
• Bootstrap preview: Resample rows with replacement, refit lm() each time, collect the slope or the prediction at a chosen \(x\), then take percentiles for a 95% interval.

What is the bootstrap (quick review)

• Goal: estimate how much a statistic (like the slope \(b_1\)) can vary from sample to sample.
• Idea: pretend your dataset is the population; resample rows with replacement, same size \(n\).
• Do many times: each resample gives a new fitted line and a new slope.
• Use the spread: the distribution of bootstrapped slopes shows your uncertainty.

Bootstrap steps you’ll do

1. Resample the rows with replacement (size \(n\))
   
2. Refit lm(y ~ x) on that resample
   
3. Store the slope \(b_1\)
   
4. Repeat (e.g., 1000–5000 times)
   
5. Take the middle 95% of the slopes to get the 95% CI for the true slope

If the 95% CI includes 0, we don’t have evidence of a nonzero slope at the 5% level.

Setup

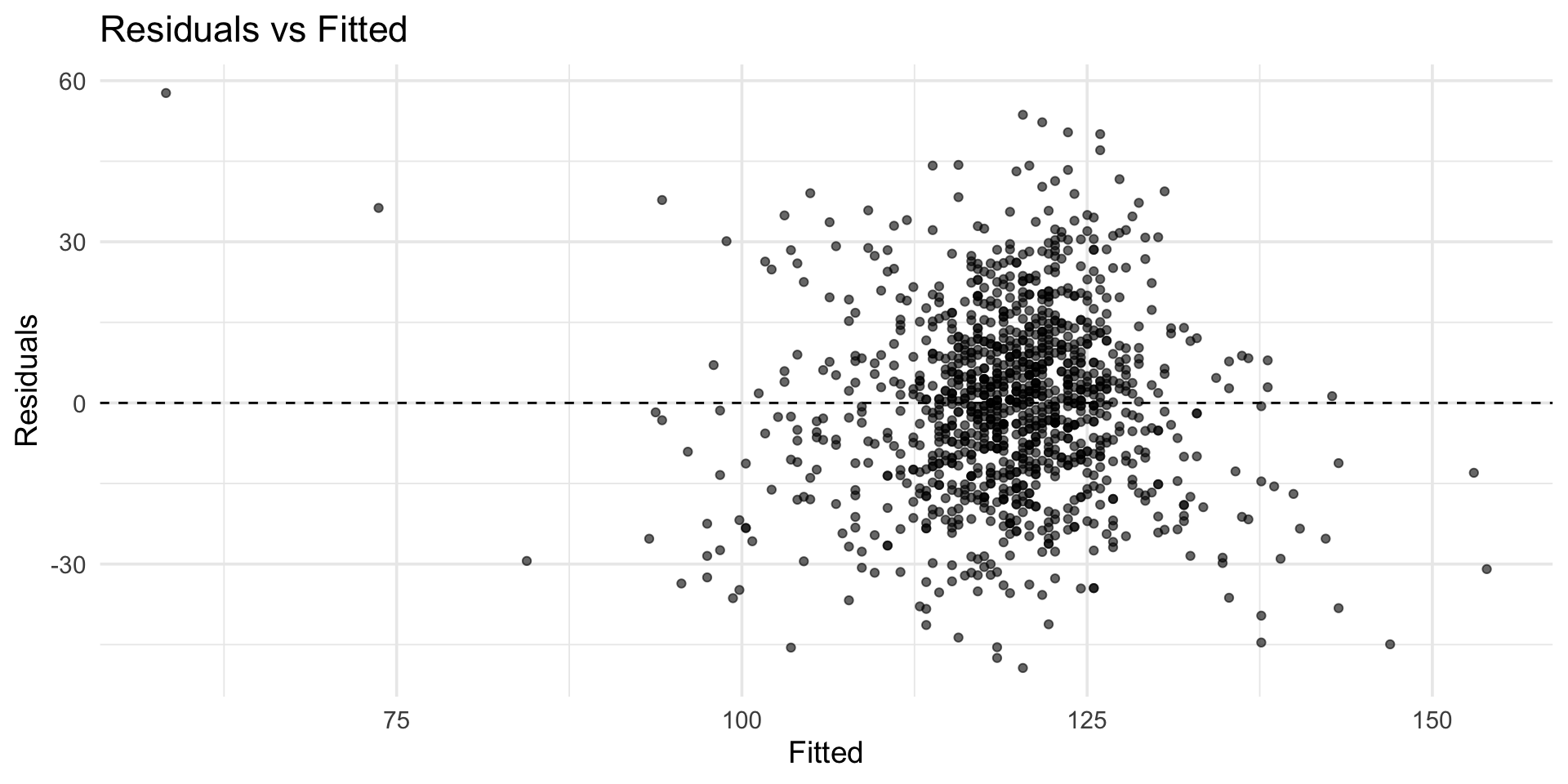
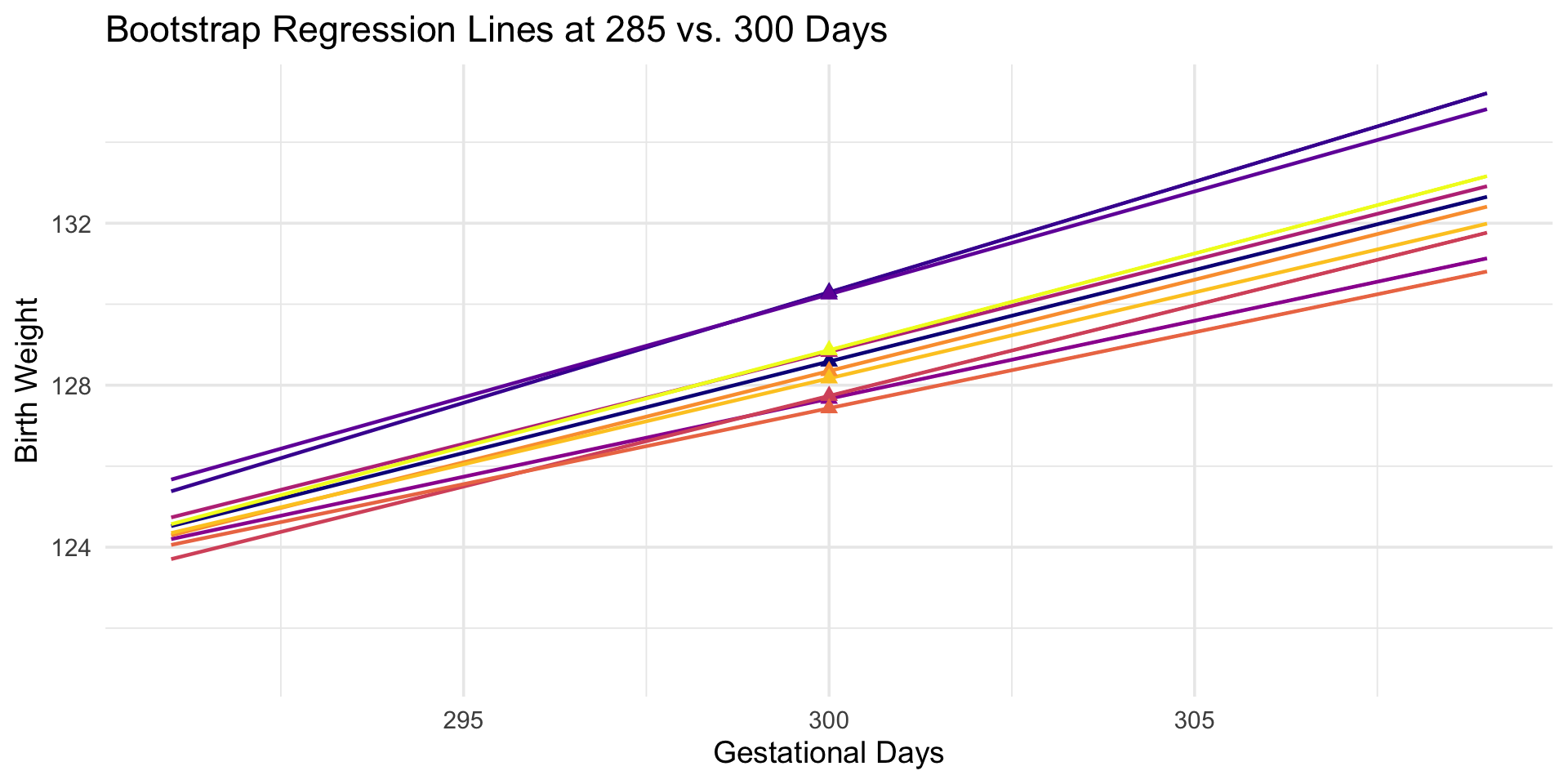
library(tidyverse)
library(infer)
library(broom)

baby <- read_csv("data/baby.csv", show_col_types = FALSE)
glimpse(baby)

Rows: 1,174
Columns: 6
$ `Birth Weight`              <dbl> 120, 113, 128, 108, 136, 138, 132, 120, 14…
$ `Gestational Days`          <dbl> 284, 282, 279, 282, 286, 244, 245, 289, 29…
$ `Maternal Age`              <dbl> 27, 33, 28, 23, 25, 33, 23, 25, 30, 27, 32…
$ `Maternal Height`           <dbl> 62, 64, 64, 67, 62, 62, 65, 62, 66, 68, 64…
$ `Maternal Pregnancy Weight` <dbl> 100, 135, 115, 125, 93, 178, 140, 125, 136…
$ `Maternal Smoker`           <lgl> FALSE, FALSE, TRUE, TRUE, FALSE, FALSE, FA…

Slope Uncertainty: Bootstrap CI

Goal: quantify uncertainty in the slope relating Birth Weight to Gestational Days.

summary <- baby |>
  summarize(
    r      = cor(`Gestational Days`, `Birth Weight`),
    slope = r * sd(`Birth Weight`) / sd(`Gestational Days`)
  )
summary

# A tibble: 1 × 2
      r slope
  <dbl> <dbl>
1 0.408 0.467

Slope Uncertainty: Bootstrap CI

set.seed(123)
boot_dist <- baby |>
  specify(`Birth Weight` ~ `Gestational Days`) |>
  generate(reps = 5000, type = "bootstrap") |>
  calculate(stat = "slope")

boot_dist |>
  ggplot(aes(x = stat)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(x = "Bootstrap Slopes", y = "Count") +
  theme_minimal(base_size = 14)

Slope Uncertainty: Bootstrap CI

ci <- boot_dist |>
  get_ci(level = 0.95, type = "percentile")
ci

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    0.378    0.560

Slope Uncertainty: Bootstrap CI

left  <- ci$lower_ci
right <- ci$upper_ci

obs_slope <- summary$slope

boot_dist |>
  ggplot(aes(x = stat)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  geom_vline(xintercept = c(left, right), linetype = "dashed", linewidth = 1) +
  geom_vline(xintercept = obs_slope, linewidth = 1) +
  labs(
    title = "Bootstrap Distribution of Slopes",
    x = "Bootstrap Slopes",
    y = "Count",
    subtitle = paste0(
      "Observed slope = ", signif(obs_slope, 4),
      " | 95% CI = [", signif(left, 4), ", ", signif(right, 4), "]"
    )
  ) +
  theme_minimal(base_size = 14)

Interpreting a Bootstrap CI for the Slope

A 95% confidence interval means:

“If we repeated the sampling process many times, about 95% of the intervals we build this way would contain the true slope.”

• If the interval for \(b_1\) includes 0, we lack strong evidence of a linear association in the population.
  
• If it does not include 0, we have evidence of a meaningful linear trend.

Test Whether There Really is a Slope

• Null hypothesis: The slope of the true line is 0.
• Alternative hypothesis: No, it’s not.
• Method:
  • Construct a bootstrap confidence interval for the true slope.
  • If the interval doesn’t contain 0, reject the null hypothesis.
  • If the interval does contain 0, there isn’t enough evidence to reject the null hypothesis.

Try it out!

names(baby)

[1] "Birth Weight"              "Gestational Days"         
[3] "Maternal Age"              "Maternal Height"          
[5] "Maternal Pregnancy Weight" "Maternal Smoker"          

• What other factors could be related to Birth Weight?

• What’s the null hypothesis? What’s your alternative hypothesis?

• Compute the confidence intervals for the following potential predictors:

  1. Maternal Age
  2. Maternal Pregnancy Weight
  3. Maternal Smoker

03:00

1. Maternal Age

boot_dist <- baby |>
  specify(`Birth Weight` ~ `Maternal Age`) |>
  generate(reps = 5000, type = "bootstrap") |>
  calculate(stat = "slope")


summary <- baby |>
  summarize(
    r      = cor(`Maternal Age`, `Birth Weight`),
    slope = r * sd(`Birth Weight`) / sd(`Maternal Age`)
  )

obs_slope <- summary$slope

ci_maternal_age <- boot_dist |>
  get_ci(level = 0.95, type = "percentile")
ci_maternal_age

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1  -0.0975    0.266

2. Maternal Pregnancy Weight

boot_dist <- baby |>
  specify(`Birth Weight` ~ `Maternal Pregnancy Weight`) |>
  generate(reps = 5000, type = "bootstrap") |>
  calculate(stat = "slope")


summary <- baby |>
  summarize(
    r      = cor(`Maternal Pregnancy Weight`, `Birth Weight`),
    slope = r * sd(`Birth Weight`) / sd(`Maternal Pregnancy Weight`)
  )

obs_slope <- summary$slope

ci_maternal_weight <- boot_dist |>
  get_ci(level = 0.95, type = "percentile")
ci_maternal_weight

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1   0.0818    0.192

3. Maternal Smoker

# Convert 'TRUE' into 1s and 'FALSE' into 0s.
baby <- baby |>
  mutate(`Maternal Smoker` = as.numeric(`Maternal Smoker`))


boot_dist <- baby |>
  specify(`Birth Weight` ~ `Maternal Smoker`) |>
  generate(reps = 5000, type = "bootstrap") |>
  calculate(stat = "slope")


summary <- baby |>
  summarize(
    r      = cor(`Maternal Smoker`, `Birth Weight`),
    slope = r * sd(`Birth Weight`) / sd(`Maternal Smoker`)
  )

obs_slope <- summary$slope

ci_maternal_smoker <- boot_dist |>
  get_ci(level = 0.95, type = "percentile")
ci_maternal_smoker

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    -11.4    -7.17

Prediction Uncertainty

• Every new prediction has random noise — individual outcomes won’t fall exactly on the line.
  
• Even if the slope were known perfectly, new observations would still vary around the line.
  
• Bootstrapping predictions works just like for slopes:
  • Resample the data with replacement
    
  • Refit lm() each time
    
  • Collect the predicted value \(\widehat{y}\) at a chosen \(x\)
    
  • Use the percentile range (e.g., middle 95%) as a prediction interval

Prediction Uncertainty at a Chosen x

We now bootstrap predicted values \(\widehat{y}\) at \(x_0 = 300\) gestational days.

x0 <- 300

set.seed(123)
boot_dist <- baby |>
  specify(`Birth Weight` ~ `Gestational Days`) |>
  generate(reps = 5000, type = "bootstrap") |>
  group_by(replicate) |>
  nest() |>
  mutate(
    model = map(data, ~ lm(`Birth Weight` ~ `Gestational Days`, data = .x)),
    yhat  = map_dbl(model, ~ predict(.x, newdata = tibble(`Gestational Days` = x0)))
  ) |>
  select(replicate, yhat)

glimpse(boot_dist)

Rows: 5,000
Columns: 2
Groups: replicate [5,000]
$ replicate <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ yhat      <dbl> 127.4013, 129.9699, 127.5875, 129.4374, 130.0132, 128.9934, …

Prediction Uncertainty at a Chosen x

boot_dist |>
  ggplot(aes(x = yhat)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(x = "Bootstrap predictions at x = 300", y = "Count",
       title = "Prediction variability via bootstrap") +
  theme_minimal(base_size = 14)

Prediction Uncertainty at a Chosen x

ci <- boot_dist |>
  rename(stat = yhat) |>
  get_ci(level = 0.95, type = "percentile")

ci

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     127.     131.

Confidence vs Prediction Intervals

Type	What It Describes	Width	Includes Random Noise?
Confidence Interval (CI)	Mean predicted response \(\widehat{y}\)	Narrower	No
Prediction Interval (PI)	A new individual’s \(y\)	Wider	Yes

Every new observation has its own random noise term \(\varepsilon\), so prediction intervals must include more uncertainty.

CI vs. PI (Example Comparison)

x0 <- 300

model <- lm(`Birth Weight` ~ `Gestational Days`, data = baby)

predict(model, newdata = tibble(`Gestational Days` = x0))

       1 
129.2129 

predict(model, newdata = tibble(`Gestational Days` = x0),
        interval = "confidence", level = 0.95)

       fit      lwr    upr
1 129.2129 127.6359 130.79

predict(model, newdata = tibble(`Gestational Days` = x0),
        interval = "prediction", level = 0.95)

       fit     lwr      upr
1 129.2129 96.3223 162.1035

Visual: Line + Prediction Marker

fit <- lm(`Birth Weight` ~ `Gestational Days`, data = baby)
fit_300 <- predict(fit, newdata = tibble(`Gestational Days` = 300))

ggplot(baby, aes(`Gestational Days`, `Birth Weight`)) +
  geom_point(alpha = 0.7, color = "chartreuse4") +
  geom_smooth(method = "lm", se = FALSE, color = "goldenrod2", linewidth = 1) +
  geom_segment(aes(x = 300, xend = 300, y = 0, yend = fit_300),
               color = "red", linewidth = 1.1) +
  labs(title = "Fitted line and prediction at x = 300",
       x = "Gestational Days", y = "Birth Weight") +
  theme_minimal(base_size = 14)

Why Check Assumptions?

Our bootstrap and analytical intervals both assume:

• A roughly linear relationship
  
• Constant spread (homoskedasticity) across \(x\)
  
• Residuals centered near 0
  
• No single outlier or leverage point dominates

If these aren’t met:

• The CI for \(b_1\) may be inaccurate
  
• The PI may be too narrow or misleading

Residual Diagnostics

fit <- lm(`Birth Weight` ~ `Gestational Days`, data = baby)
aug <- augment(fit)

ggplot(aug, aes(.fitted, .resid)) +
  geom_hline(yintercept = 0, linetype = "dashed") +
  geom_point(alpha = 0.6) +
  labs(title = "Residuals vs Fitted", x = "Fitted", y = "Residuals") +
  theme_minimal(base_size = 14)

Try it out!

• Compute the bootstrap distribution for the prediction for 285 Gestational Days based on Baby Weight.
• Compute the confidence interval.
• Compute the prediction interval.
• Compare that to the results we got for 300 Gestational Days.

03:00

Discussion

Predictions Near vs. Far from the Mean

At \(x_0 = 285\), predictions vary less than at \(x_0 = 300\).

Why?

• The mean of Gestational Days is about 279 days.

mean(baby$`Gestational Days`)

[1] 279.1014

• Predictions near the center of \(x\) values are more stable — most bootstrap lines agree there.
  
• Predictions farther from the mean show more spread, since small slope differences create larger changes in \(\widehat{y}\).

Summary

• Predictions are most stable near the mean of \(x\).
  
• Farther from the mean means more uncertainty in \(\widehat{y}\).
  
• Use bootstrap to see this variability directly.
  
• Always distinguish:
  • CI: uncertainty in the average prediction
    
  • PI: uncertainty in a new individual’s prediction