Classification

November 18, 2025

Big Picture Recap

• So far, we have focused on prediction/estimation using linear regression.
• We used features (inputs, \(X\)) to predict an outcome (response, \(Y\)).
• Today we:
  • Connect regression to classification.
  • Set up a machine learning framework for training and testing models.

Linear Regression (Recap)

• Goal: predict a numeric outcome \(Y\) from one or more predictors \(X\).

• Examples:

  • Predict exam score from hours studied.
  • Predict body mass from flipper length.

• Setup:

  • Numeric \(X\) → directly into the model.
  • Categorical \(X\) → convert to numeric first, then use regression.

If \(X\) is Categorical

We encode categories as numeric variables.

• Binary category:
  • Convert to 0/1 and proceed with regression.
  • Example: Smoker
    • Smoker = 0 for “No”
    • Smoker = 1 for “Yes”

If \(X\) is Categorical

• Multi-level categorical predictors:
  • Use one-hot encoding (indicator / dummy variables).
  • Example: Color with levels: Red, Blue, Green
    • Create:
      • Color_Blue = 1 if Blue, 0 otherwise
        
      • Color_Green = 1 if Green, 0 otherwise
        
    • Baseline: Red (when both indicators are 0).
  • One-hot encoding turns categories into vectors (e.g., Red = (0,0), Blue = (1,0), Green = (0,1))

Multiple Linear Regression

• Extends simple linear regression to multiple predictors.
• Goal: predict a numeric outcome \(Y\) using several features:

\[\widehat{Y} = b_0 + b_1 X_1 + b_2 X_2 + \dots + b_p X_p\]

model <- lm(exam_score ~ hours_studied + hours_slept, data = my_data)
summary(model)

Many factors can contribute to an outcome.

Guessing the Value of a Variable

• Based on incomplete information
• One way of making predictions / estimate:
  • To predict an outcome for an individual,
  • find others who are like that individual
  • and whose outcomes you know.
  • Use those outcomes as the basis of your prediction.
• Two Types of Prediction
  • Regression = Numeric; Classification = Categorical

Classification

02:00

Spam or not spam? Why do you think so?

Machine Learning Algorithm

• A mathematical model
• calculated based on sample data
  • “training data”
• that makes predictions or decisions without being explicitly programmed to perform the task

Classification Examples: Text

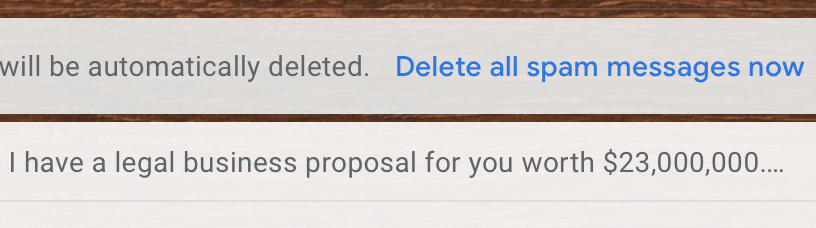
Output: (Spam, Not Spam)

Classification Examples: Image

Output: (Car, Road, Tree, Sky, Traffic Sign)

Classification Examples: Image

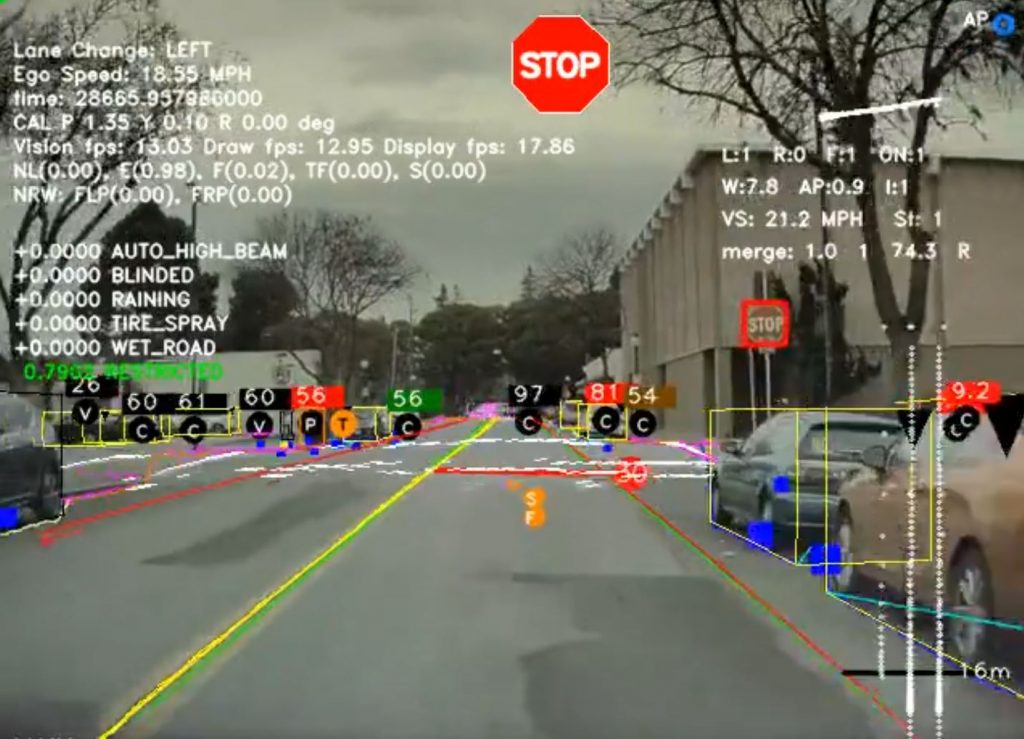
Output: (Car, Road, Tree, Sky, Traffic Sign)

Classification Examples: Videos

Output: (In, Out)

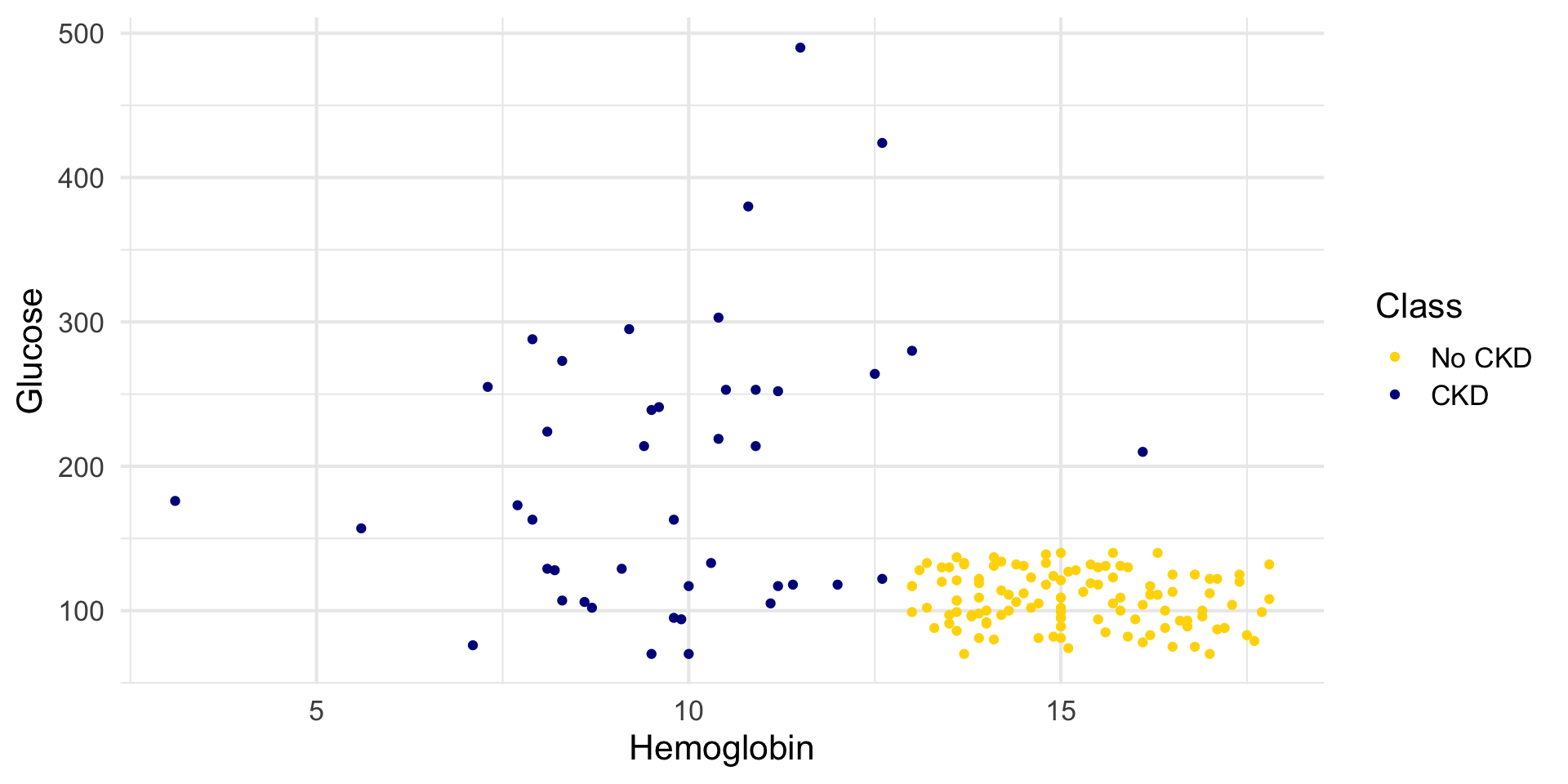
CKD Data

library(readr)
library(dplyr)
ckd <- read_csv("data/ckd.csv") |>
  rename(Glucose = `Blood Glucose Random`) |>
  mutate(
    Class = factor(
      Class,
      levels = c(0, 1),
      labels = c("No CKD", "CKD")
    )
  )

ckd |> count(Class)

# A tibble: 2 × 2
  Class      n
  <fct>  <int>
1 No CKD   115
2 CKD       43

Hemoglobin and Glucose

library(ggplot2)

ggplot(ckd, aes(x = Hemoglobin, y = Glucose, color = Class)) +
  geom_point() +
  scale_color_manual(
    values = c("No CKD" = "gold", "CKD" = "darkblue")
  ) +
  theme_minimal(base_size = 16)

White Blood Cell Count and Glucose

ggplot(ckd, aes(x = `White Blood Cell Count`, y = Glucose, color = Class)) +
  geom_point() +
  scale_color_manual(
    values = c("No CKD" = "gold", "CKD" = "darkblue")
  ) +
  theme_minimal(base_size = 16)

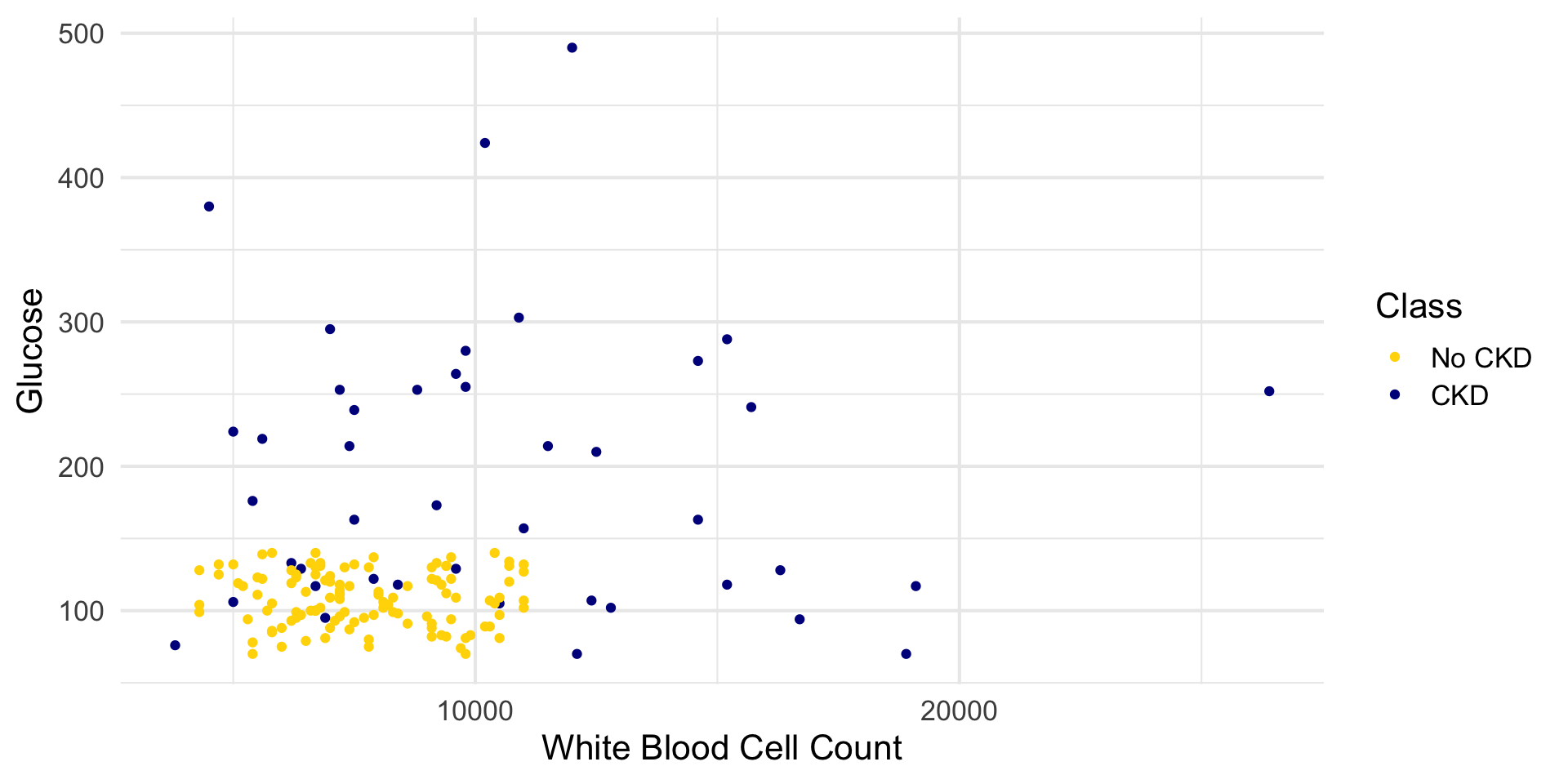
Manual Classfier

max_gluc_0 <- ckd |>
  filter(Class == "No CKD") |>
  summarize(max_glucose = max(Glucose)) |>
  pull(max_glucose)

min_hemo_0 <- ckd |>
  filter(Class == "No CKD") |>
  summarize(min_hemo = min(Hemoglobin)) |>
  pull(min_hemo)

max_gluc_0

[1] 140

min_hemo_0

[1] 13

Manual Classfier

classify_manually <- function(hemoglobin, glucose) {
  if (hemoglobin < min_hemo_0 || glucose > max_gluc_0) {
    return(1)
  } else {
    return(0)
  }
}

classify_manually(15, 100)

[1] 0

classify_manually(10, 300)

[1] 1

Classifiers

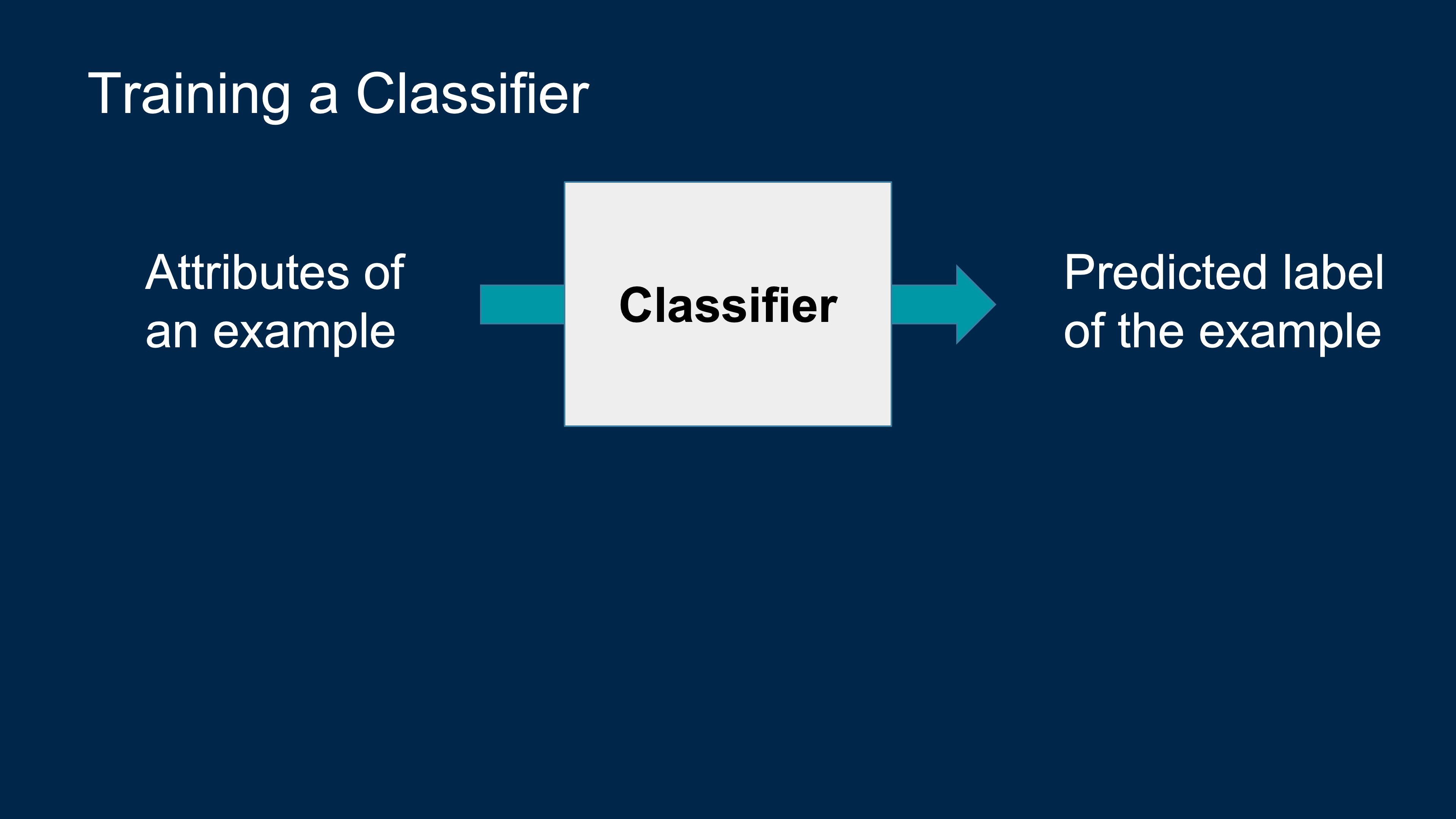
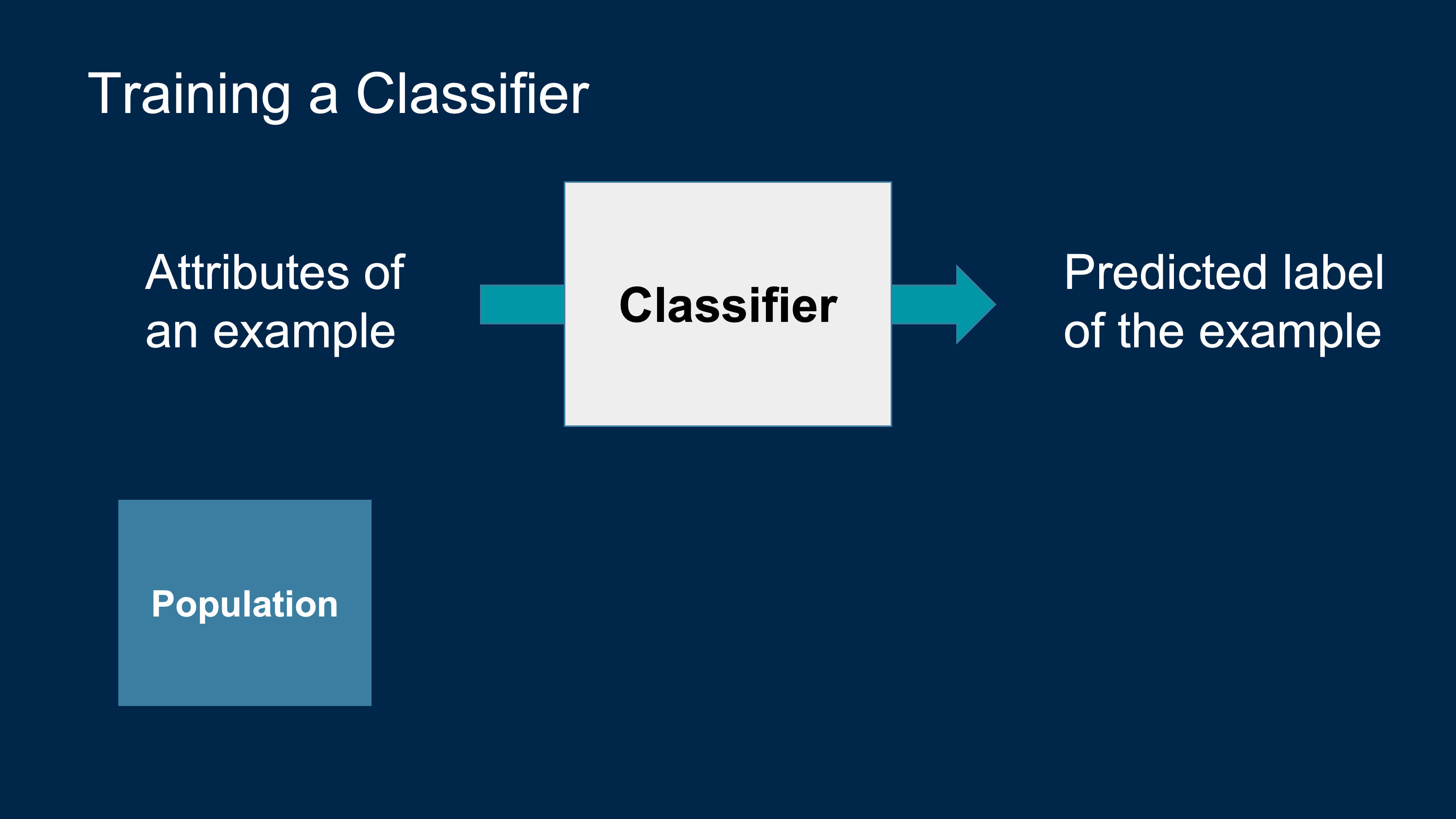
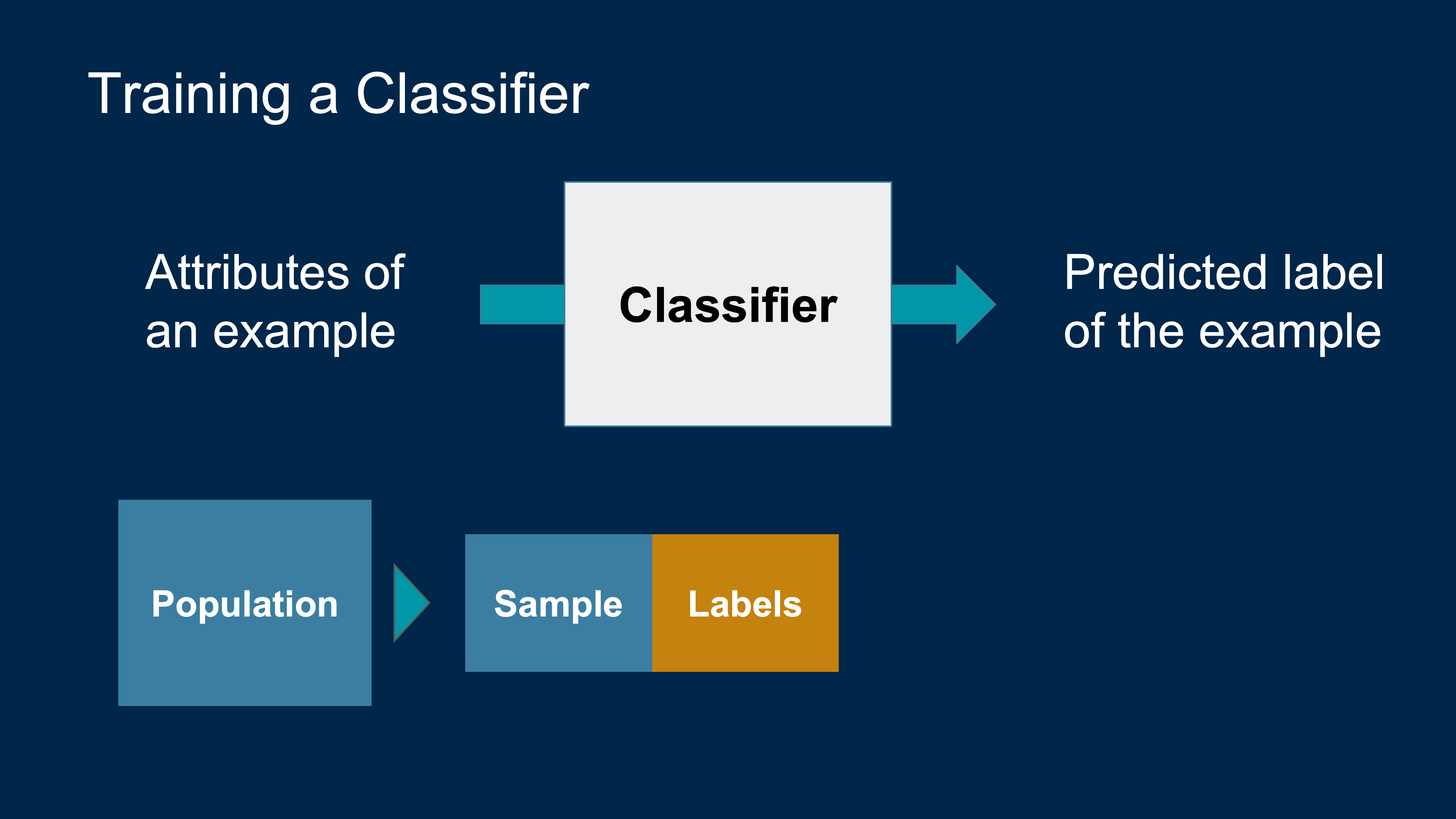
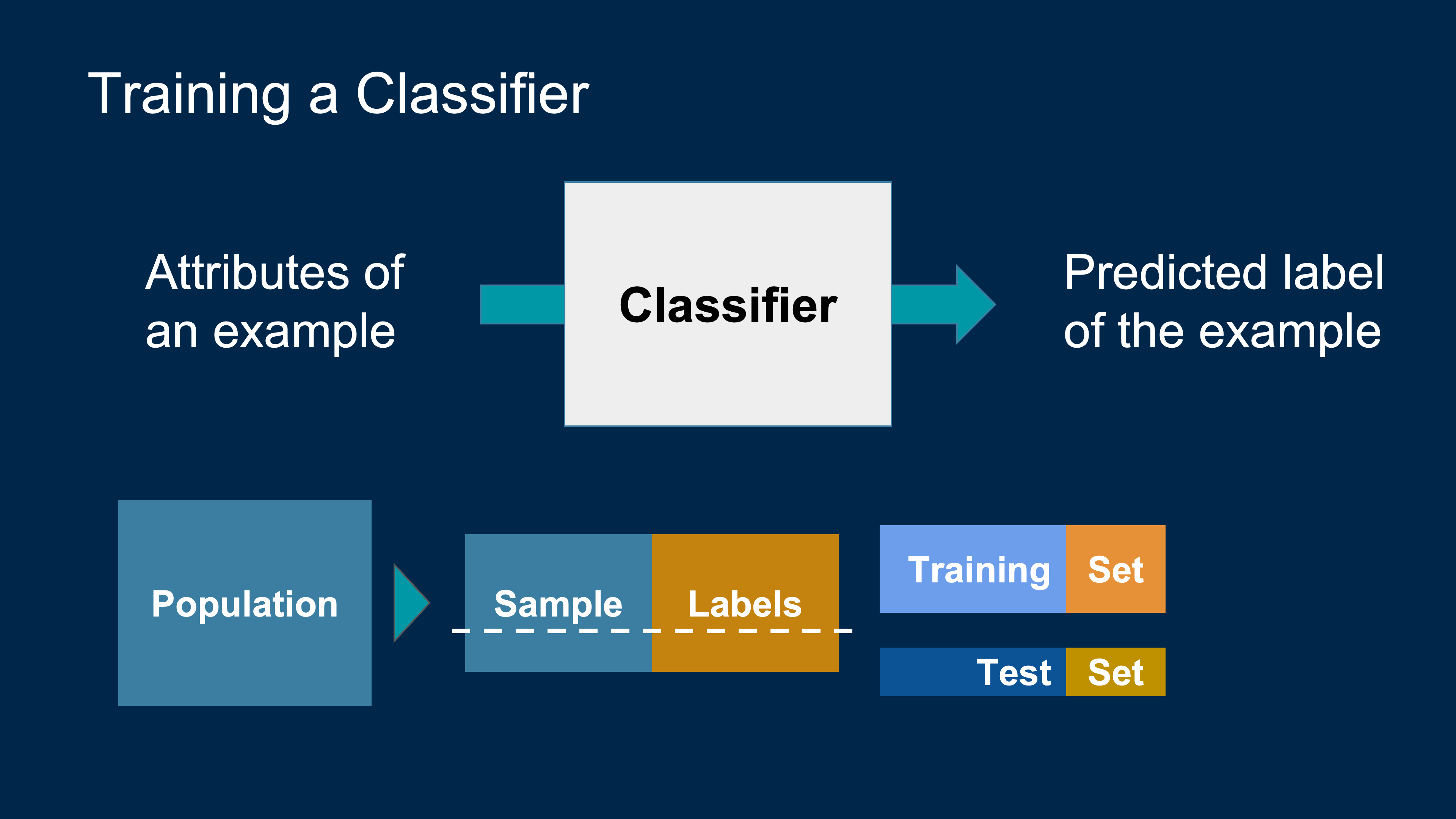
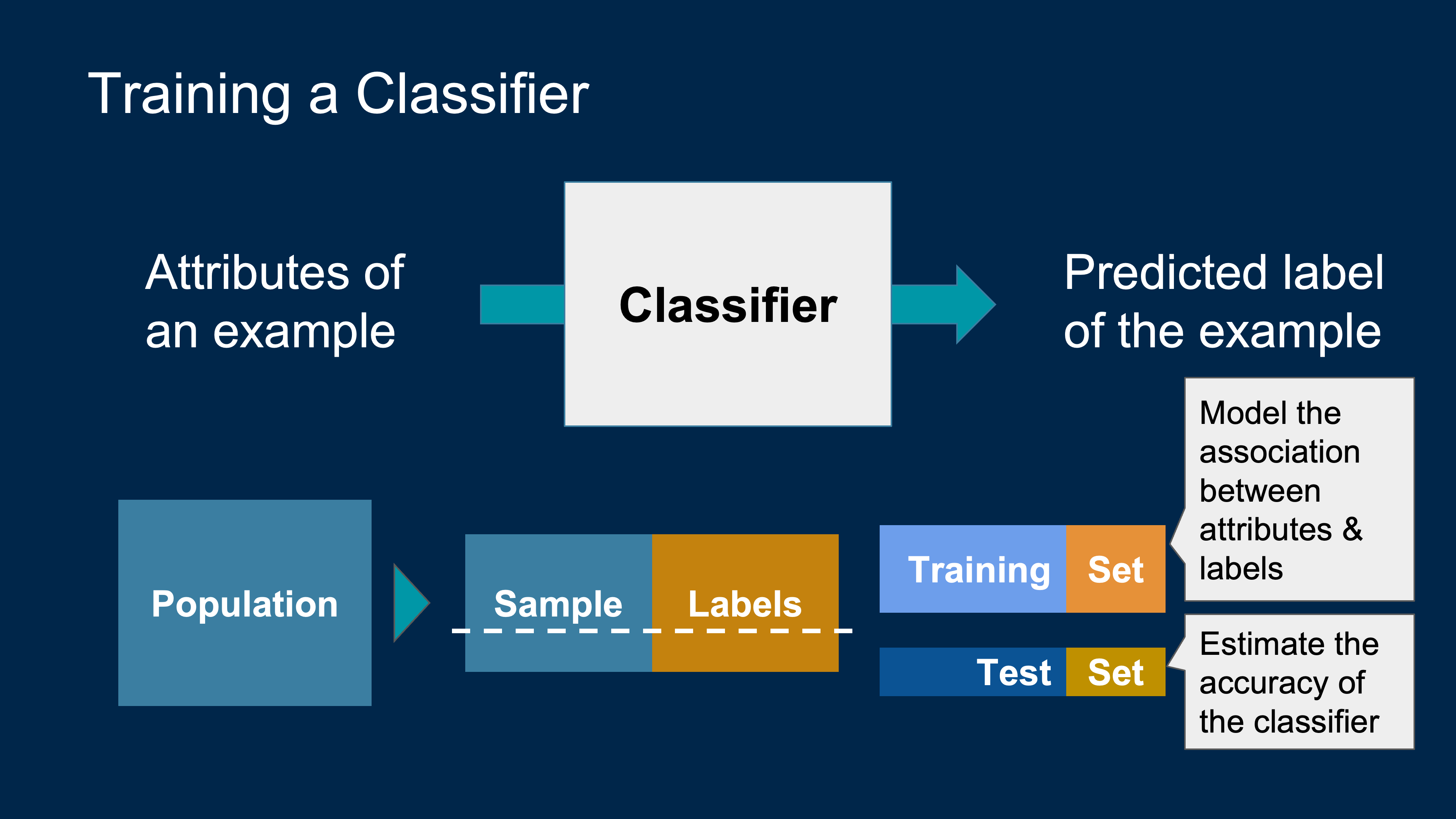
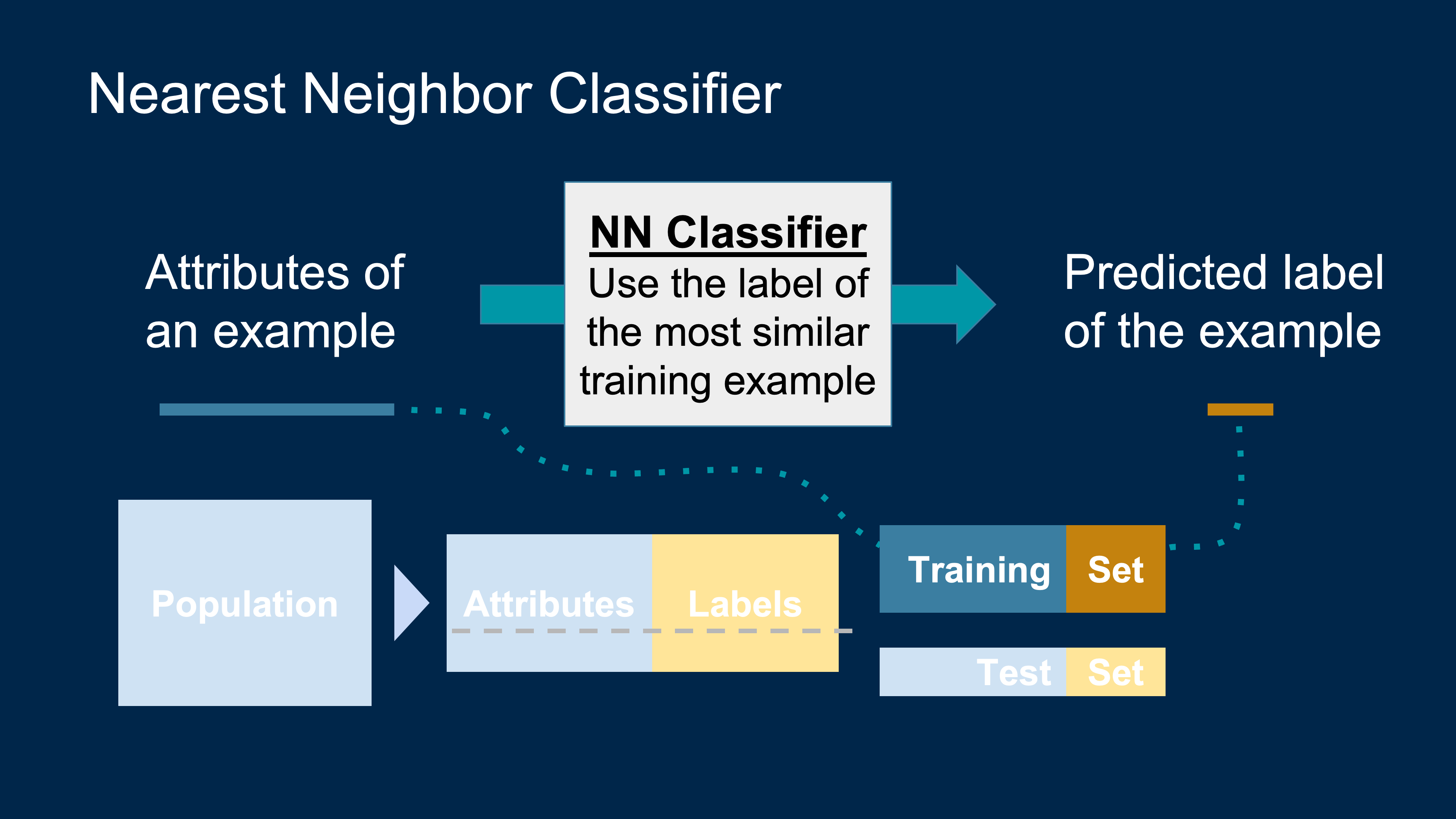
Regression vs Classification (Summary)

• Regression:
  • Output: numeric \(Y\) (e.g., income, temperature, score).
  • Model: usually a line or curve.
  • Fit by minimizing squared errors.
• Classification:
  • Output: category (e.g., spam / not spam).
  • Model: decision boundary between classes.
  • Fit by minimizing classification errors (or related loss).