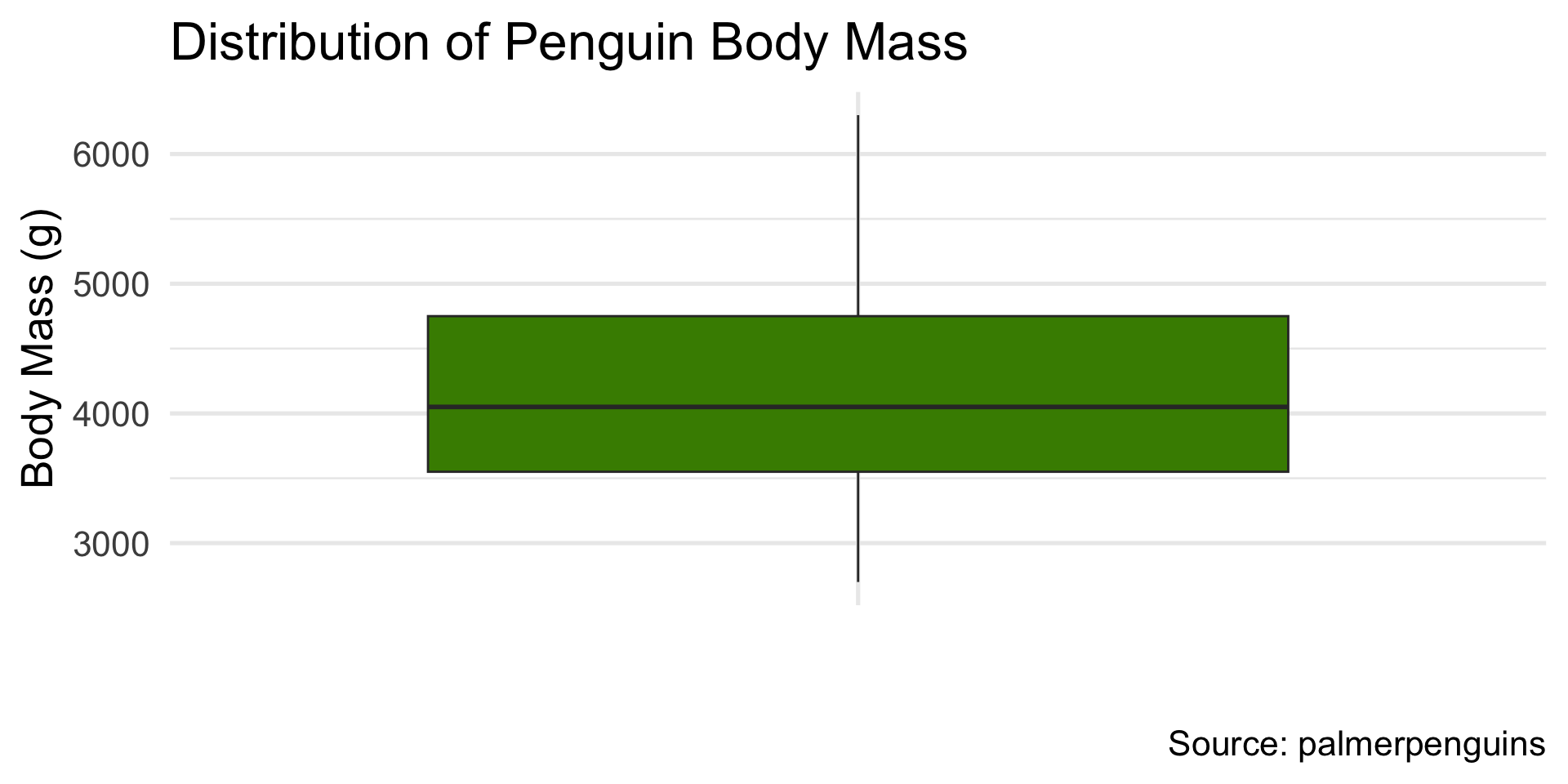Describing Distributions

Sarah Cassie Burnett

October 14, 2025

Why Probability Distributions?

• In real data, we often don’t have all the information about a population.
• Instead, we collect random samples and use probability to reason about them.
• Probability distributions describe how likely different outcomes are.

Uniform Distribution

Rolling a Die

• Outcomes / states: x = 1, 2, 3, 4, 5, 6
  
• Each outcome has equal probability: \[ \begin{aligned} P(x = 1) &= P(x = 2) = P(x = 3) = P(x = 4) \\[4pt] &= P(x = 5) = P(x = 6) = \frac{1}{6} \approx 0.1666667 \end{aligned} \]

The probability of rolling a 1, 2, 3, 4, 5, or 6 with a fair die is equal for each outcome.

Outcomes vs. Events

Outcome:

• A single possible result of an experiment.
  
• Example: rolling a 4 on a fair die.

Event:

• A collection or condition involving one or more outcomes.
  
• Example: rolling an even number → {2, 4, 6}.
  
• Probability of this event: \(P(x\text{ is even}) = \frac{3}{6} = 0.5\)

Outcomes are individual results; Events are groups of outcomes we assign probabilities to.

Uniform Distribution

Let’s Roll One!

• We could roll a real die, but it would take a while to collect enough data.
• Instead, we’ll simulate rolls in R.

sample(1:6, size = 1)

[1] 5

Simulation is the process of using a computer to mimic a physical experiment.

Uniform Distribution

Simulate rolling die

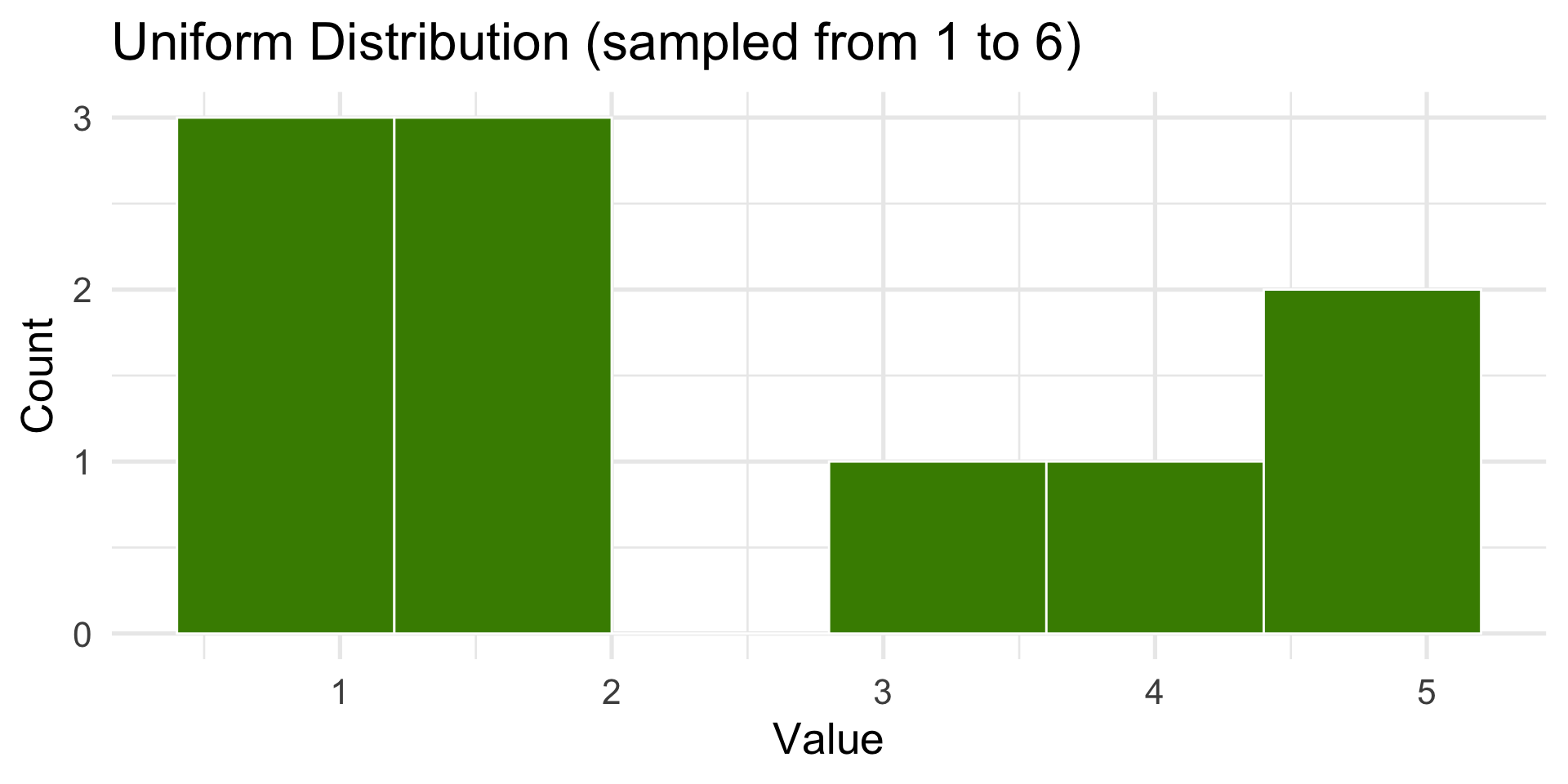
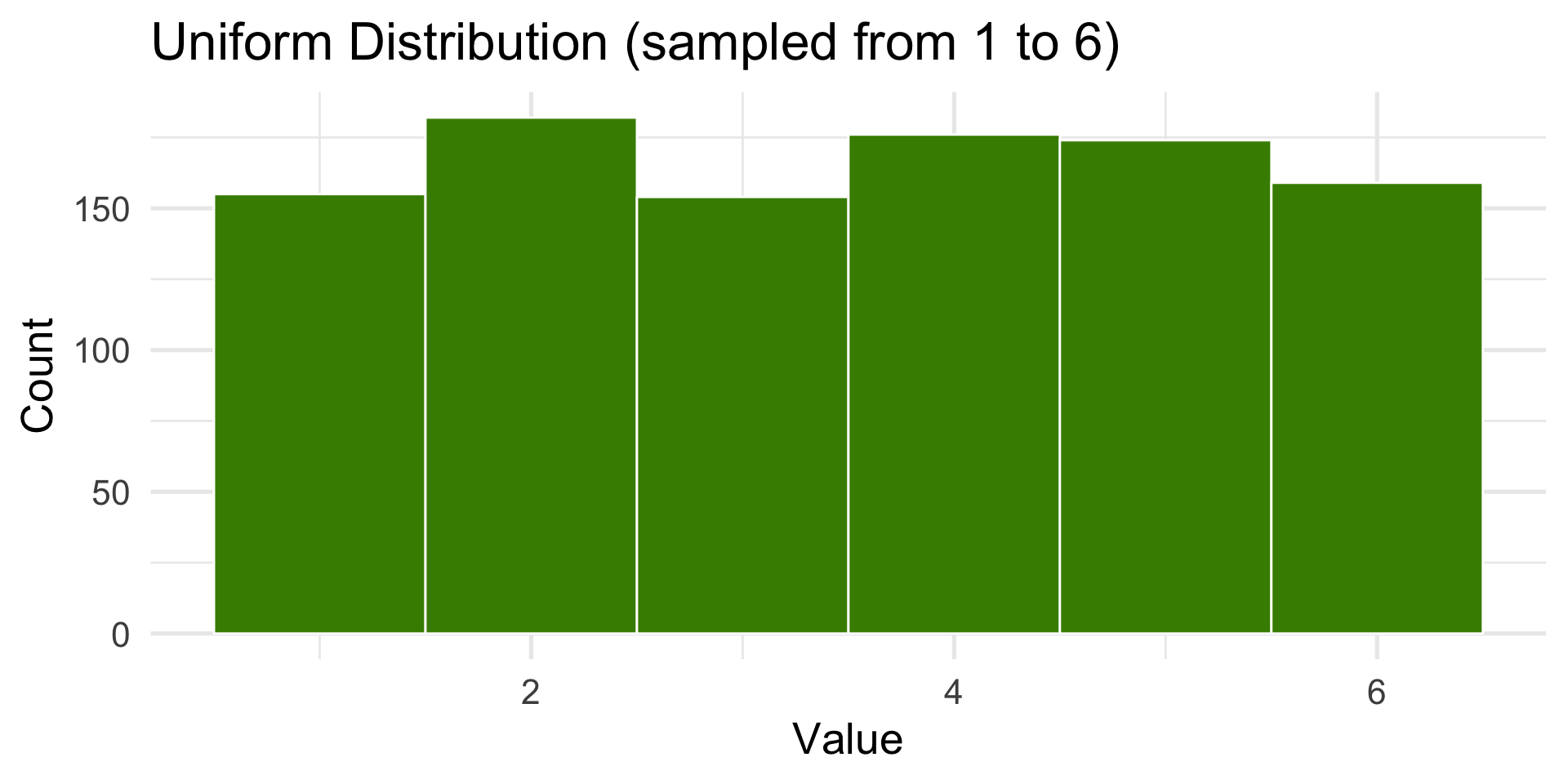
Let’s simulate 10 die rolls… 1000 die rolls.

rolls <- sample(1:6, size = 10, replace = TRUE)
rolls

 [1] 1 2 2 6 3 3 2 3 5 6

The Law of Large Numbers (LLN) is a fundamental principle in probability and statistics that describes how the results of random events become more predictable as the number of trials increases.

Uniform Distribution

10 die rolls

library(tidyverse)

N <- 10

dist <- tibble(x = sample(1:6, size = N, replace = TRUE))
ggplot(dist, aes(x)) +
  geom_histogram(bins = 6, fill = "chartreuse4", color = "white") +
  labs(
    title = "Uniform Distribution (sampled from 1 to 6)",
    x = "Value",
    y = "Count"
  ) + theme_minimal(base_size = 20)

Uniform Distribution

1000 die rolls

set.seed(7)
N <- 1000

dist <- tibble(x = sample(1:6, size = N, replace = TRUE))
ggplot(dist, aes(x)) +
  geom_histogram(bins = 6, fill = "chartreuse4", color = "white") +
  labs(
    title = "Uniform Distribution (sampled from 1 to 6)",
    x = "Value",
    y = "Count"
  )+ theme_minimal(base_size = 20)

Uniform Distribution

1000 die rolls as a proportion

set.seed(7)
N <- 1000

dist <- tibble(x = sample(1:6, size = N, replace = TRUE))
hist <- ggplot(dist, aes(x)) +
  geom_histogram(aes(y = after_stat(count / sum(count))), bins = 6, fill = "chartreuse4", color = "white") +
  labs(
    title = "Uniform Distribution (sampled from 1 to 6)",
    x = "Value",
    y = "Proportion"
  ) + theme_minimal(base_size = 20)

hist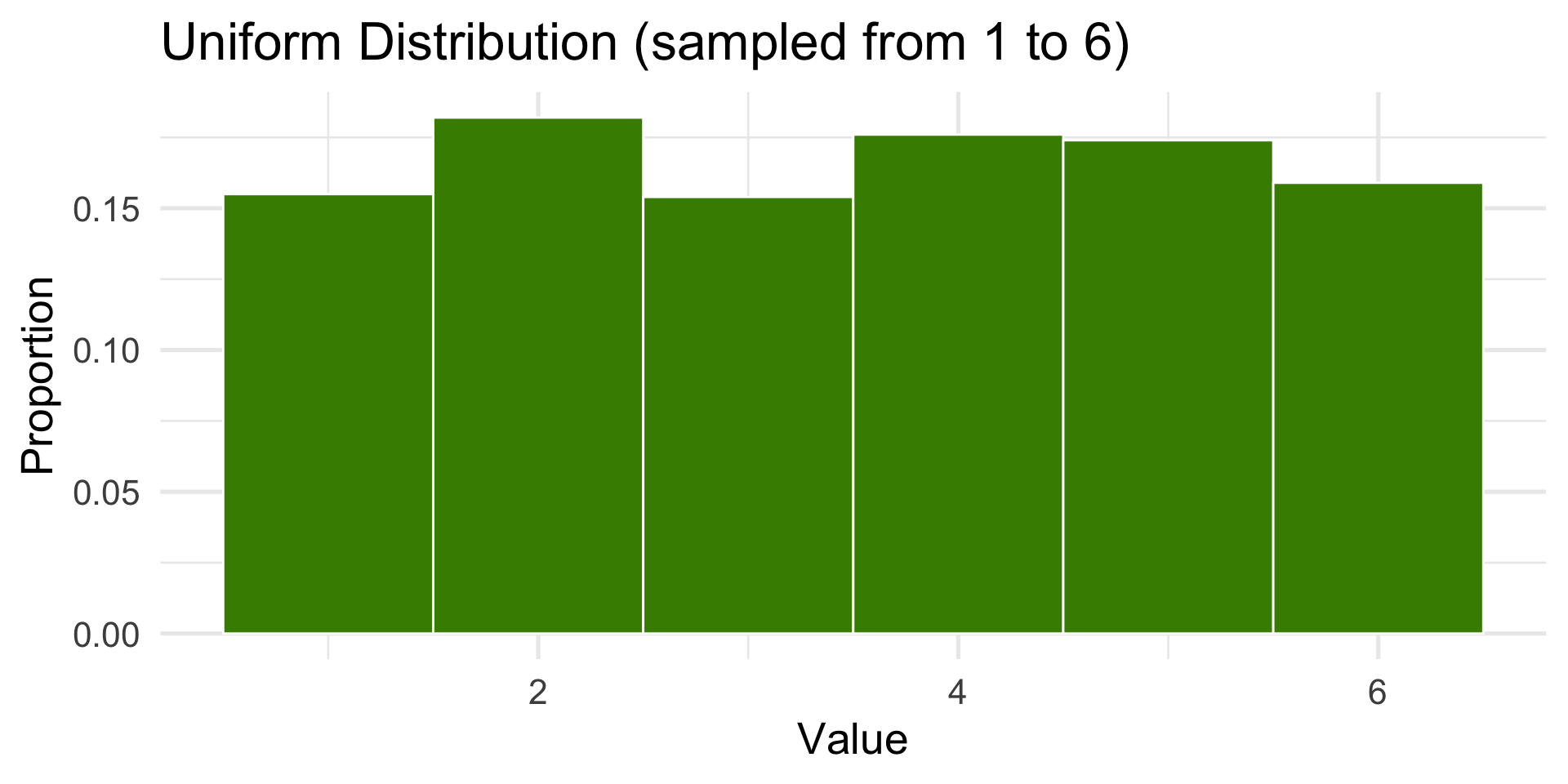

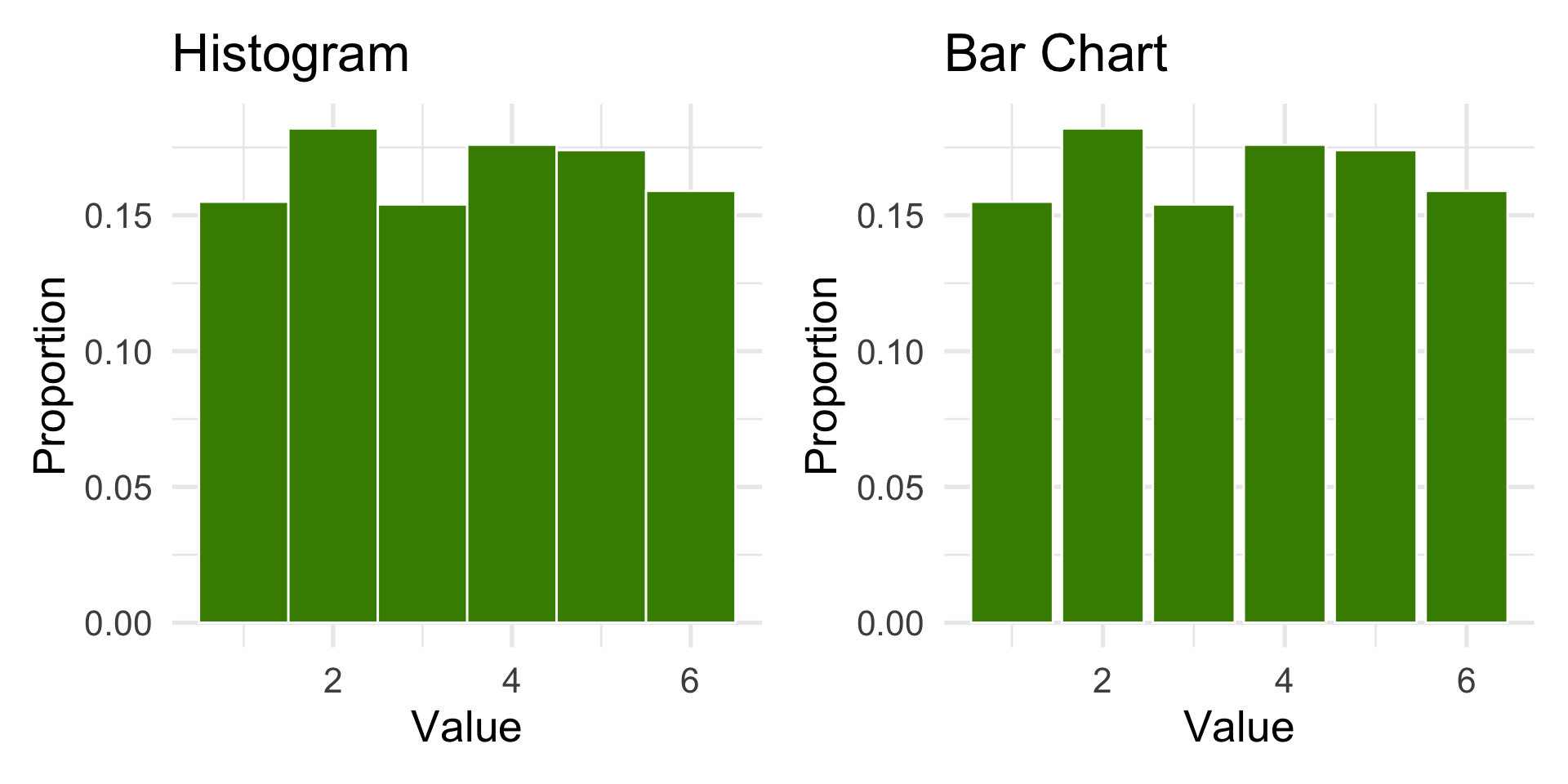
Histograms

• Used to represent the distribution of a continuous variable
• The x-axis represents the range of values
• The y-axis represents the frequency of each value
• The bars represent the number of observations in each range or “bin”
• Adjust bins and bin widths to best view the distribution
• The shape of the histogram can tell us a lot about the distribution of the data

Aside on the Die Rolls Example

• A die roll is a categorical variable: the outcomes {1, 2, 3, 4, 5, 6} are labels.
  
• The bar chart is the correct choice to display categorical frequencies.

In practice, for discrete outcomes, geom_bar() is preferred.

barc <- ggplot(dist, aes(x)) +
  geom_bar(aes(y = after_stat(count / sum(count))), fill = "chartreuse4", color = "white") +
  labs(
    title = "Bar Chart",
    x = "Value",
    y = "Proportion"
  ) + theme_minimal(base_size = 20)

hist <- hist + labs(title = "Histogram")

library(patchwork)
hist + barc

Type of Distributions

Many real-world variables follow non-uniform distributions.

In R, there are built in functions to generate these distributions:

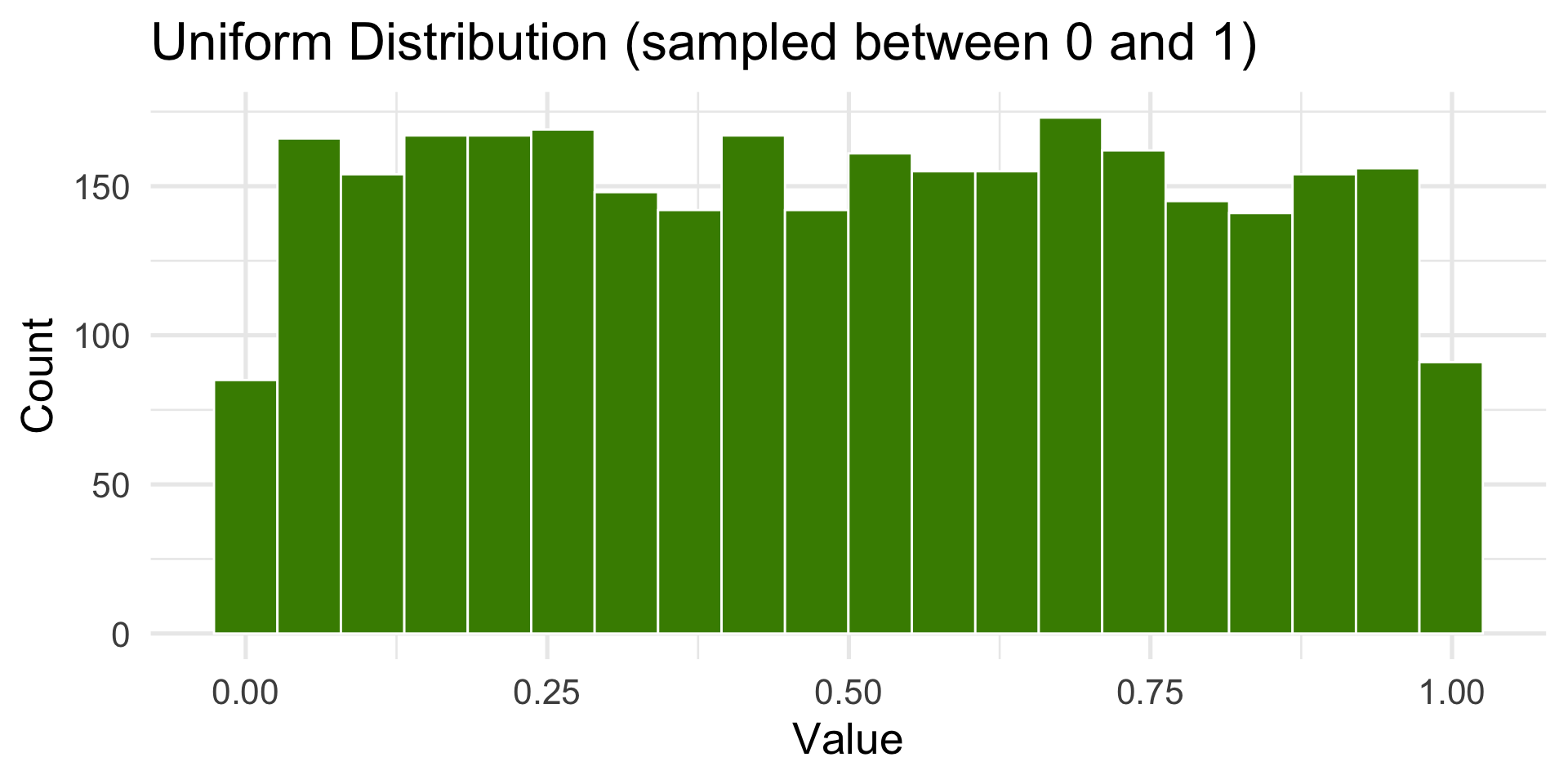
• runif() — Uniform distribution
  
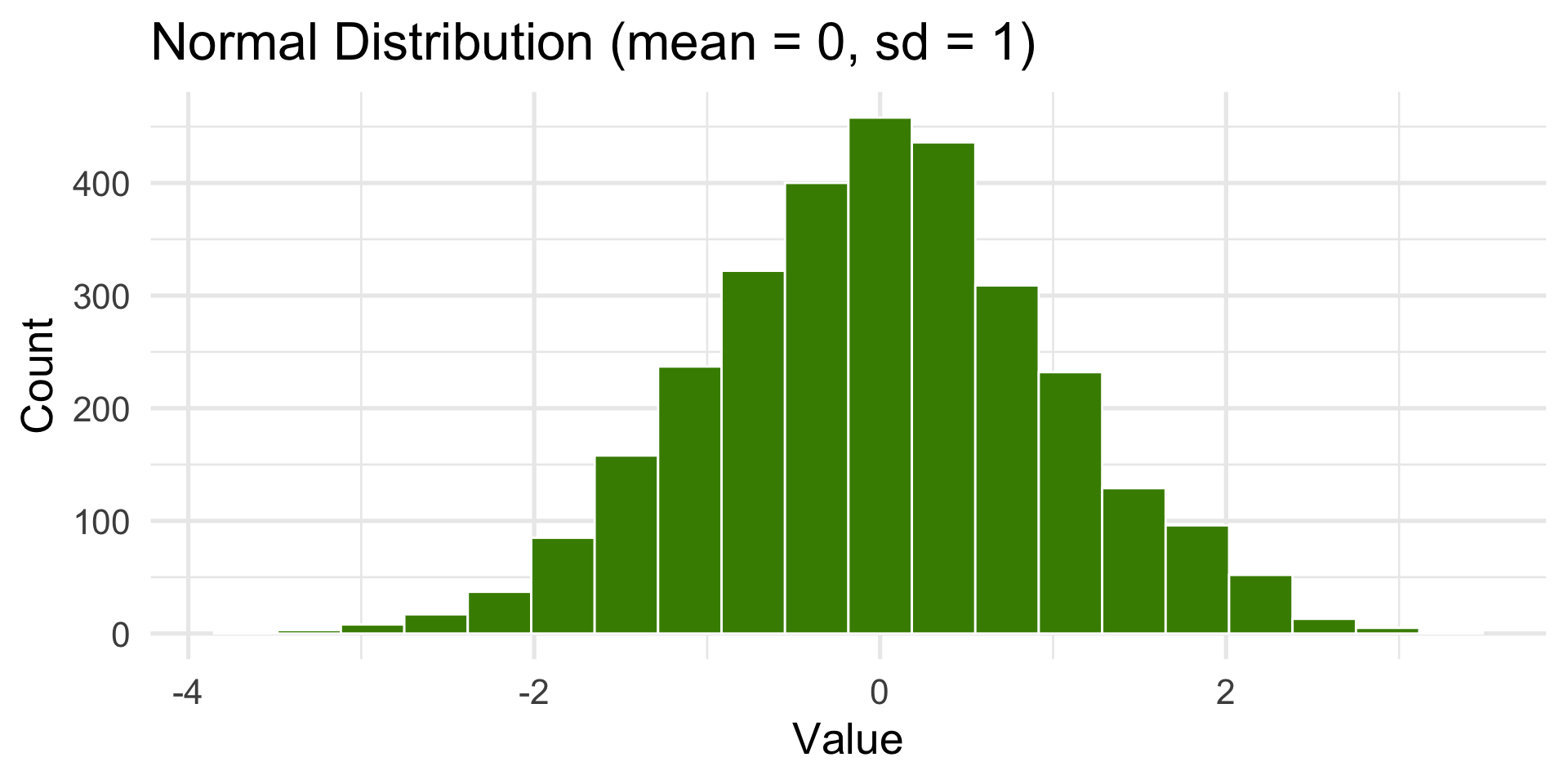
• rnorm() — Normal (Gaussian) distribution
  
• rpois() — Poisson distribution
  
• rexp() — Exponential distribution

Uniform

All outcomes are equally likely.

N <- 3000
dist <- tibble(x = runif(N, min = 0, max = 1))
ggplot(dist, aes(x)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(
    title = "Uniform Distribution (sampled between 0 and 1)",
    x = "Value",
    y = "Count"
  ) + theme_minimal(base_size = 20)

Normal or Gaussian Distribution

Also known as the bell-shaped or standard distribution.

It’s the most common distribution in statistics and math.

dist <- tibble(x = rnorm(N, mean = 0, sd = 1))
ggplot(dist, aes(x)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(title = "Normal Distribution (mean = 0, sd = 1)",
       x = "Value", y = "Count") + theme_minimal(base_size = 20)

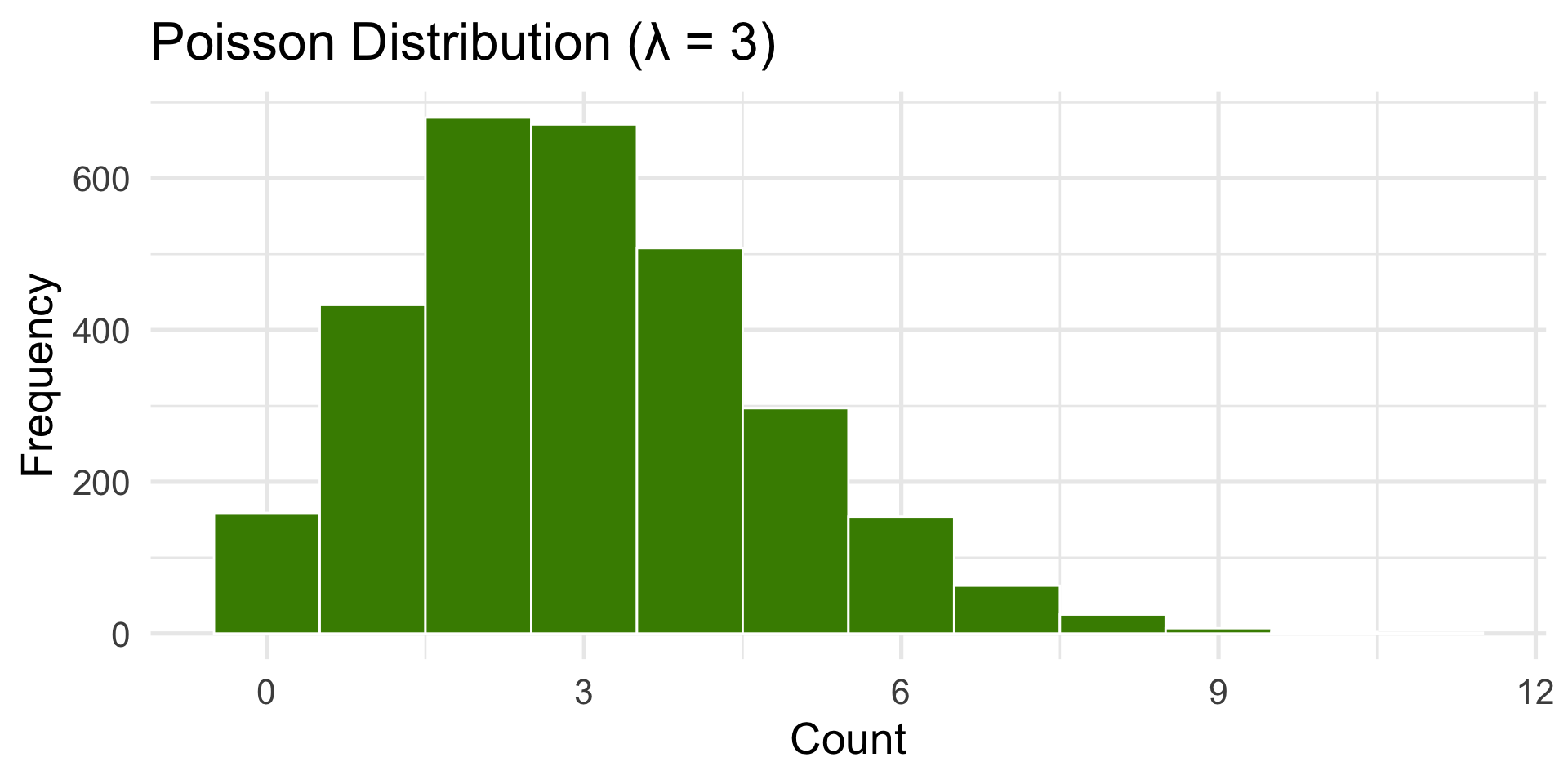
Poisson Distribution

Used for counts of random, independent events.

(e.g., number of emails per hour or bus arrivals.)

dist <- tibble(x = rpois(N, lambda = 3))
ggplot(dist, aes(x)) +
  geom_histogram(binwidth = 1, fill = "chartreuse4", color = "white") +
  labs(title = "Poisson Distribution (λ = 3)",
       x = "Count", y = "Frequency") + theme_minimal(base_size = 20)

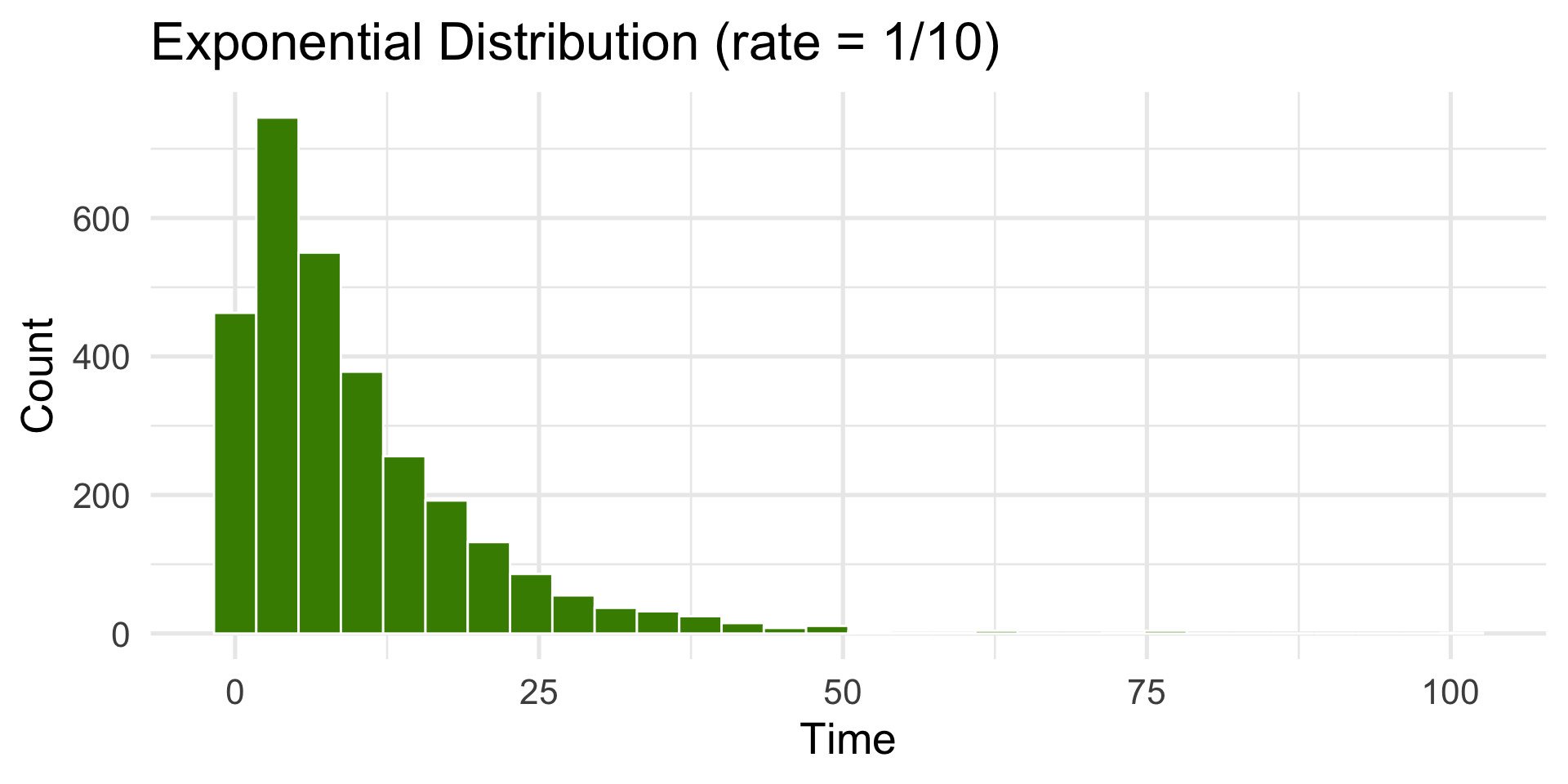
Exponential Distribution

Used for waiting times between random events.

dist <- tibble(x = rexp(N, rate = 1/10))
ggplot(dist, aes(x)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white") +
  labs(title = "Exponential Distribution (rate = 1/10)",
       x = "Time", y = "Count") + theme_minimal(base_size = 20)

Describing Distribution Shape

• Number of peaks (modes): unimodal, bimodal, multimodal
  

Describing Distribution Shape

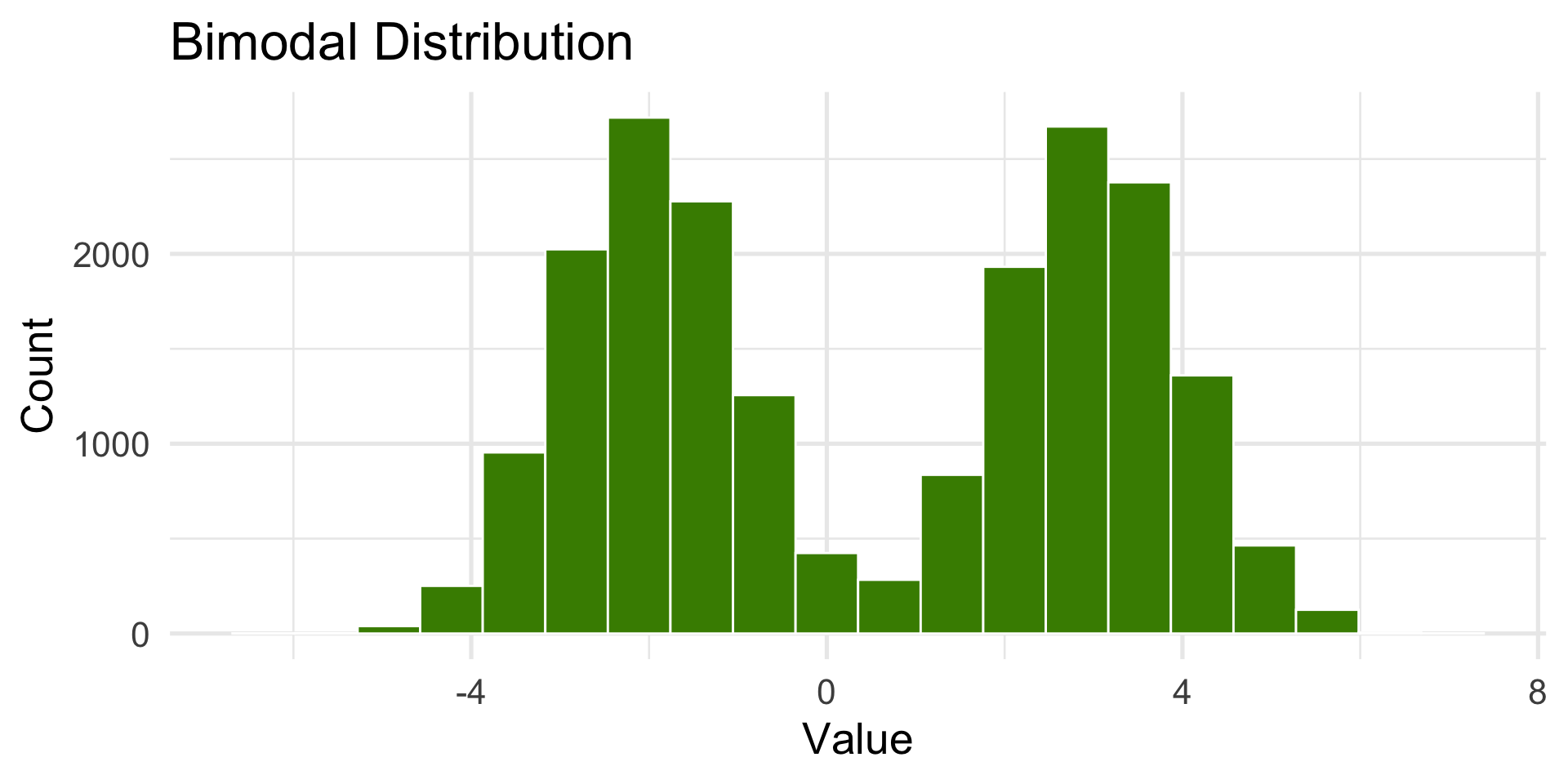
Bimodal Distribution

• Two peaks (like two distributions are combined).

Describing Distribution Shape

• Number of peaks (modes): unimodal, bimodal, multimodal
  
• Direction of skew: left-skewed or right-skewed

Describing Distribution Shape

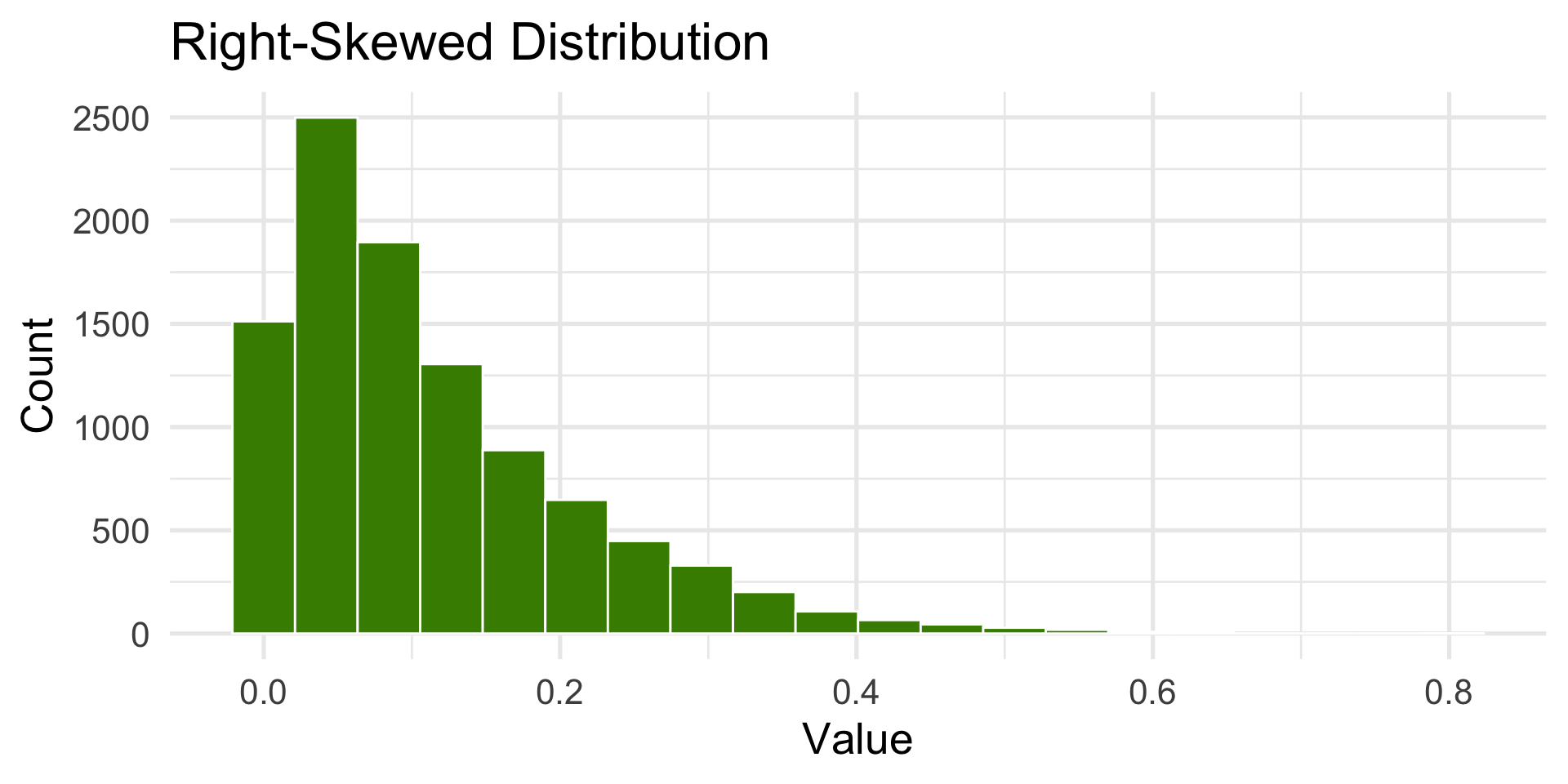
Right-Skewed Distribution

• Tail extends to the right.

Describing Distribution Shape

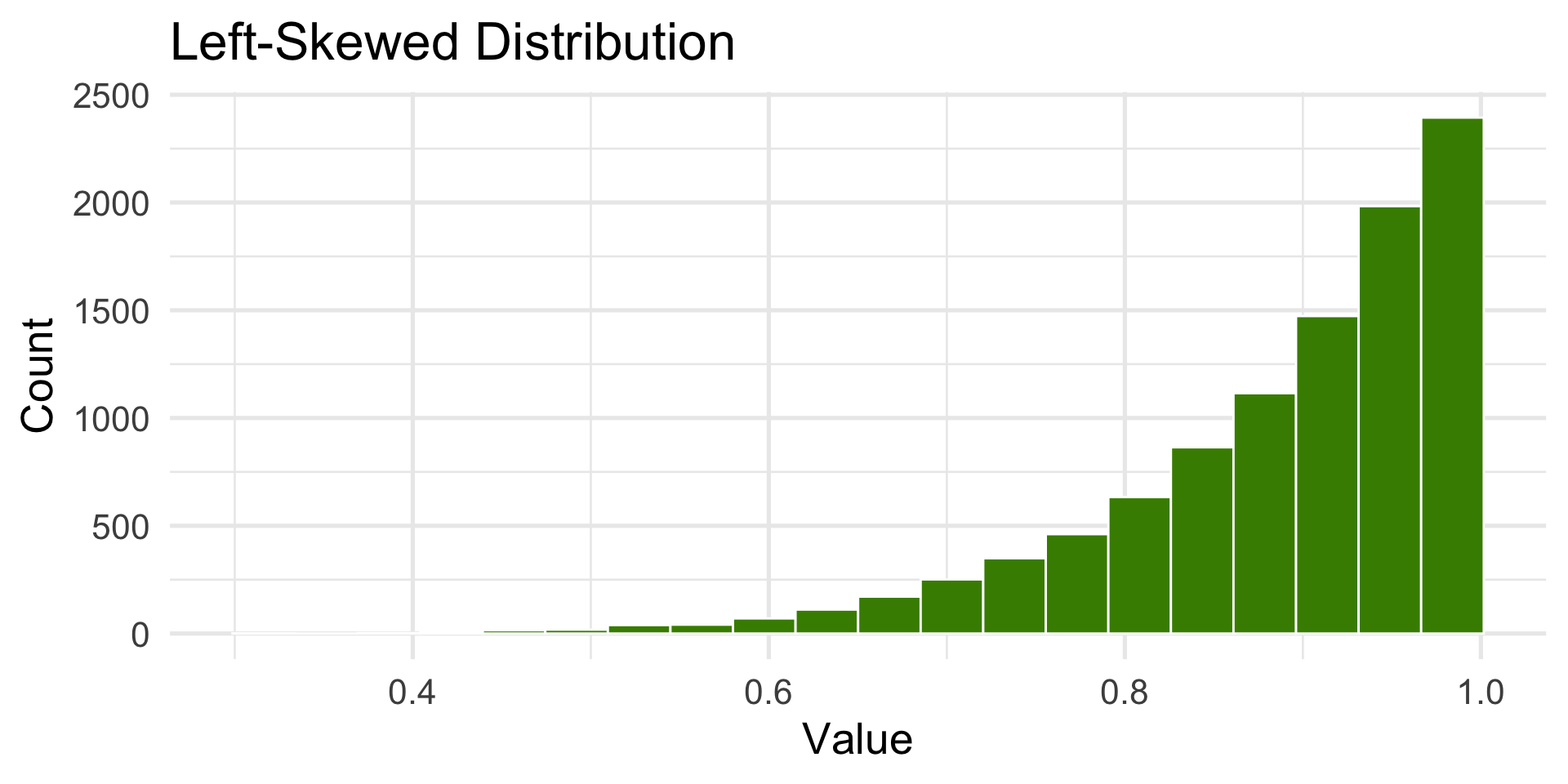
Left-Skewed Distribution

• Tail extends to the left.

Try it out with real data!

Which describe the shape each variable:

1. palmerpenguins::penguins$body_mass_g (body mass of penguins).
   
2. faithful$waiting (waiting time between Old Faithful eruptions).
3. ggplot2::diamonds$price (price of diamonds).

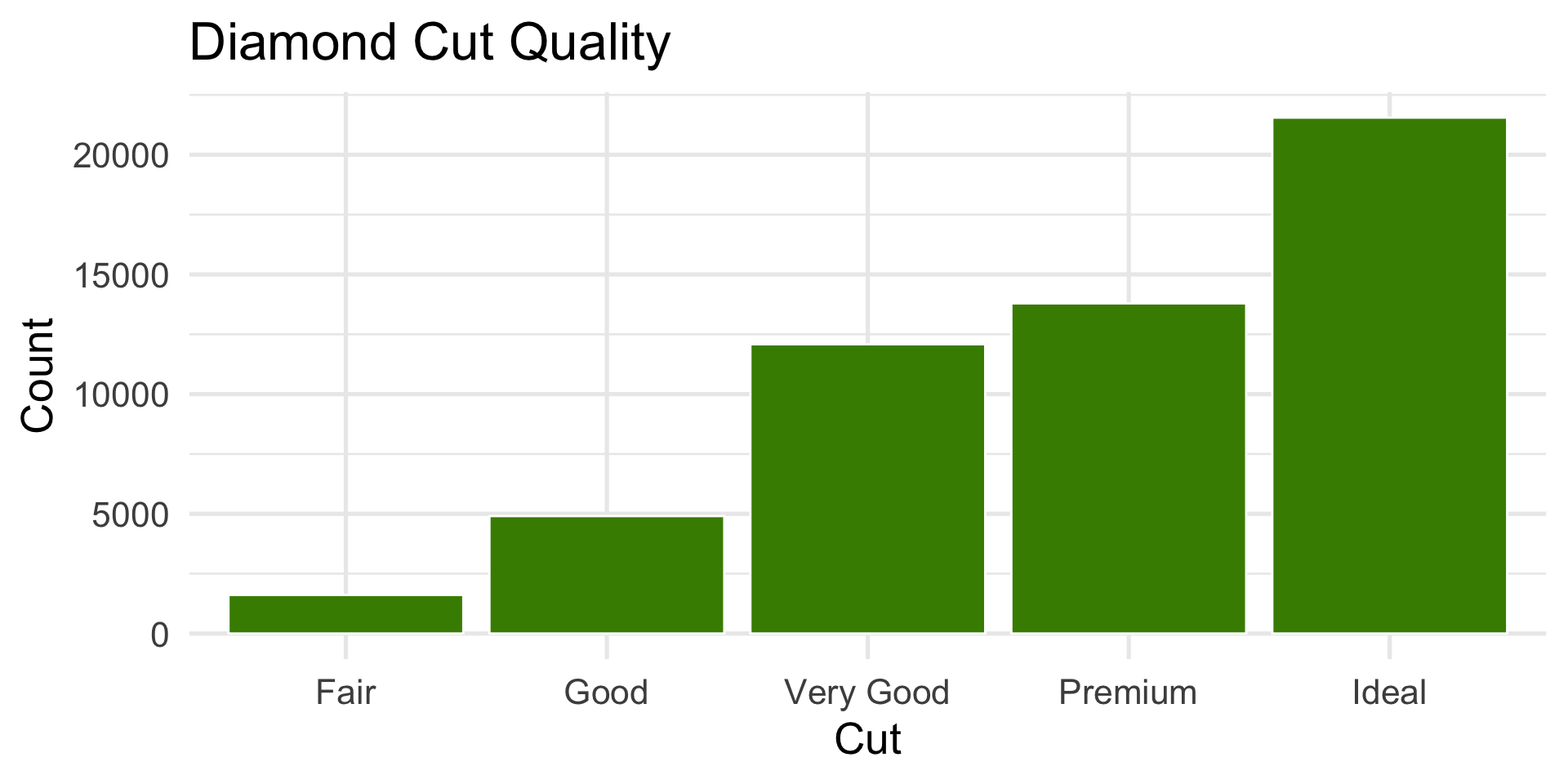
Challenge: How would you describe ggplot2::diamonds$cut (cut of diamonds)?

(See the next slide for the code for the plots.)

05:00

Code for activity

#1
library(palmerpenguins)
ggplot(penguins, aes(x = body_mass_g)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(title = "Penguin Body Mass", x = "Body Mass (g)", y = "Count")

#2
ggplot(faithful, aes(x = waiting)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white") +
  labs(title = "Old Faithful Waiting Times", x = "Minutes", y = "Count")

#3
ggplot(diamonds, aes(x = price)) +
  geom_histogram(bins = 50, fill = "chartreuse4", color = "white") +
  labs(title = "Diamond Prices", x = "Price (USD)", y = "Count")

#4
ggplot(diamonds, aes(x = cut)) +
  geom_bar(fill = "chartreuse4", color = "white") +
  labs(title = "Diamond Cut Quality", x = "Cut", y = "Count")

body mass of penguins

library(palmerpenguins)
ggplot(penguins, aes(x = body_mass_g)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  labs(title = "Penguin Body Mass", x = "Body Mass (g)", y = "Count")+ theme_minimal(base_size = 20)

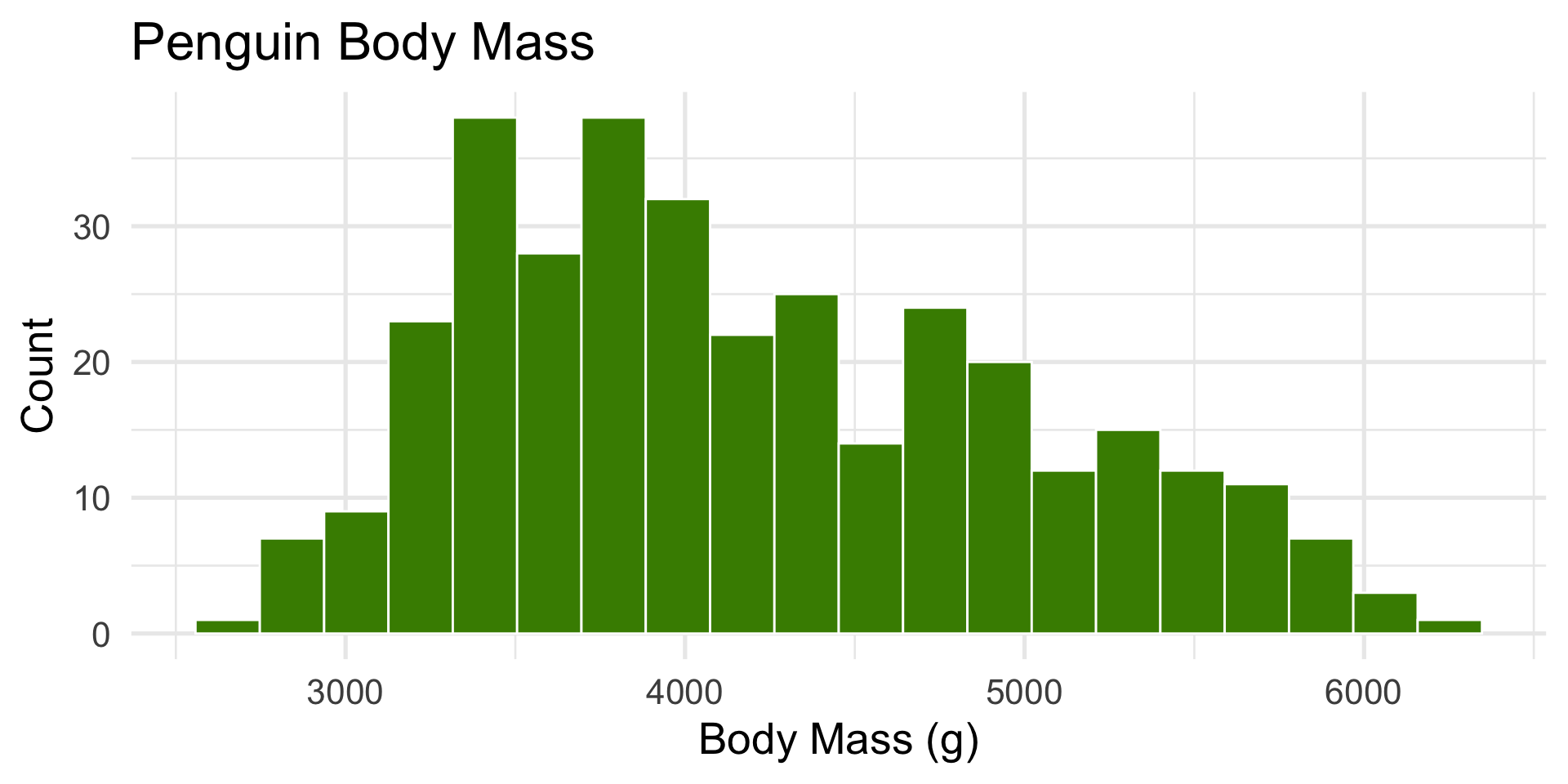
• Slightly right-skewed — heavier penguins pull the tail.

waiting time between Old Faithful eruptions

ggplot(faithful, aes(x = waiting)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white") +
  labs(title = "Old Faithful Waiting Times", x = "Minutes", y = "Count")+ theme_minimal(base_size = 20)

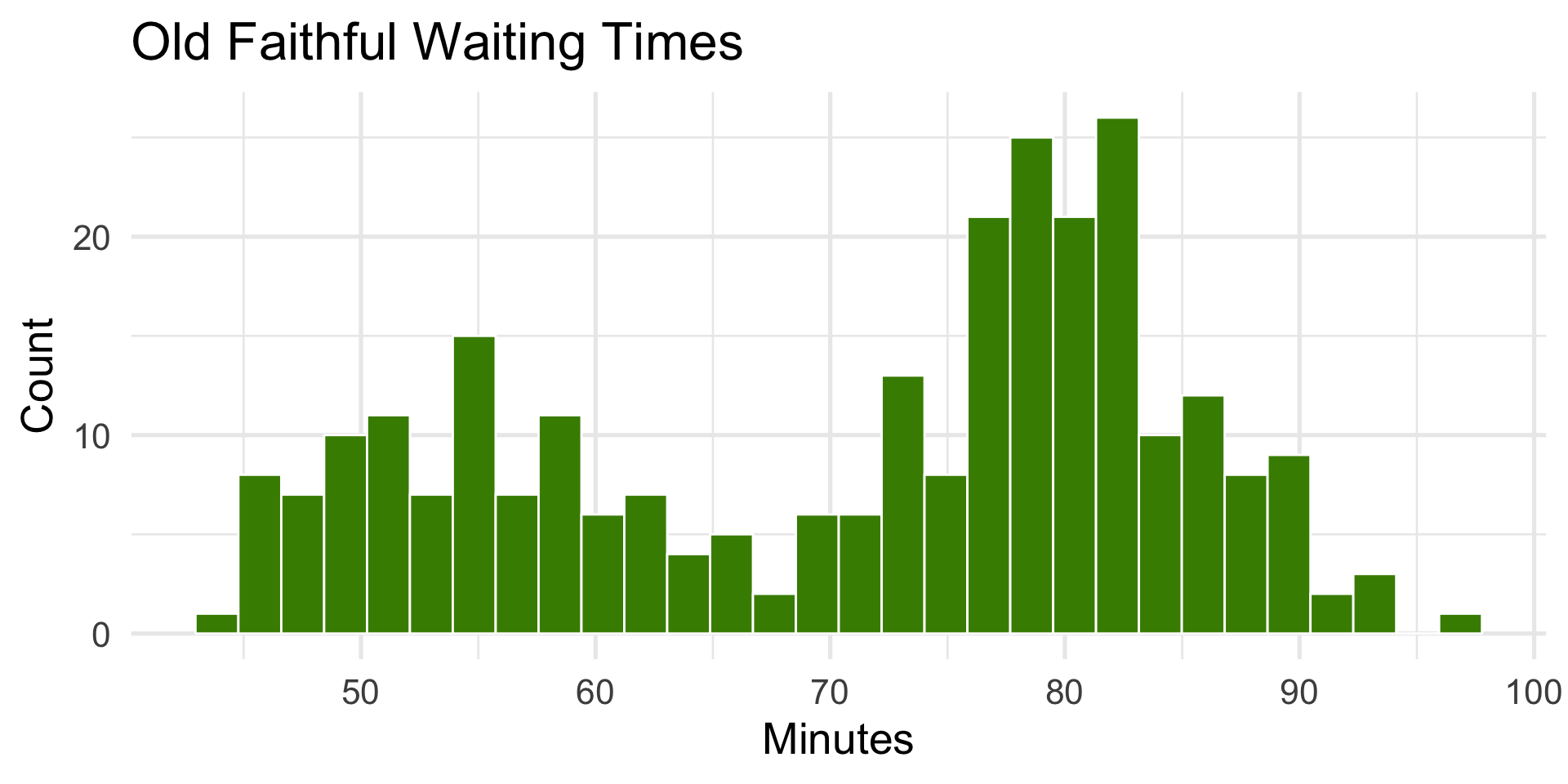
• Bimodal — two eruption types (short vs. long).

price of diamonds

ggplot(diamonds, aes(x = price)) +
  geom_histogram(bins = 50, fill = "chartreuse4", color = "white") +
  labs(title = "Diamond Prices", x = "Price (USD)", y = "Count")+ theme_minimal(base_size = 20)

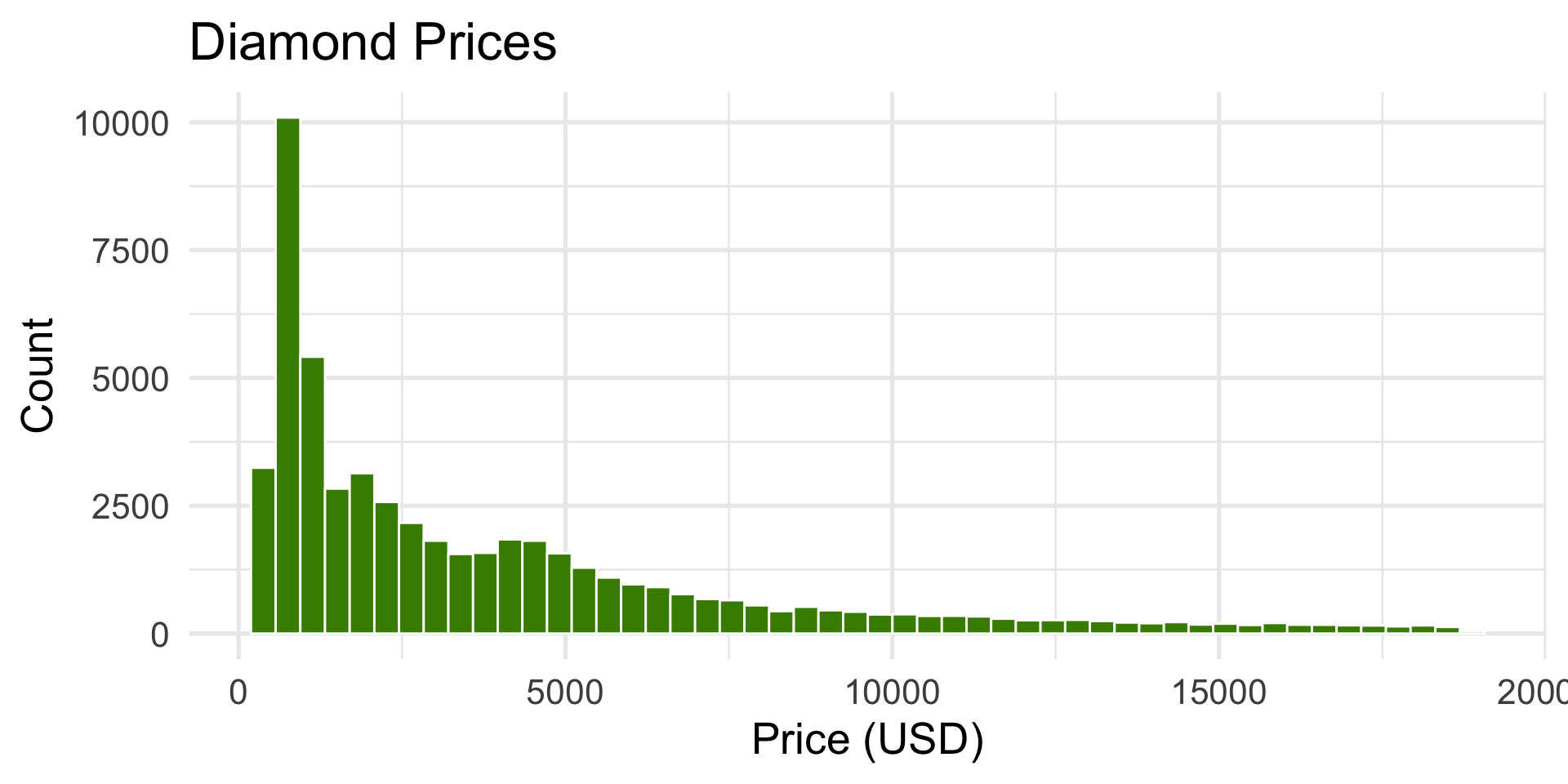
• Hard right-skewed — many small/cheap diamonds, few very expensive ones.

cut of diamonds

ggplot(diamonds, aes(x = cut)) +
  geom_bar(fill = "chartreuse4", color = "white") +
  labs(title = "Diamond Cut Quality", x = "Cut", y = "Count")+ theme_minimal(base_size = 20)

• Most diamonds are in the higher-quality categories (Ideal and Premium).
• We describe the distribution of categories, not skewness for categorical variables.

Describing Distribution Shape

• Number of peaks (modes): unimodal, bimodal, multimodal
  
• Direction of skew: left-skewed or right-skewed
  
• Symmetry: is the distribution balanced?

Symmetric distribution

• The center represents the typical (expected) value, and both tails are similar in length and shape.

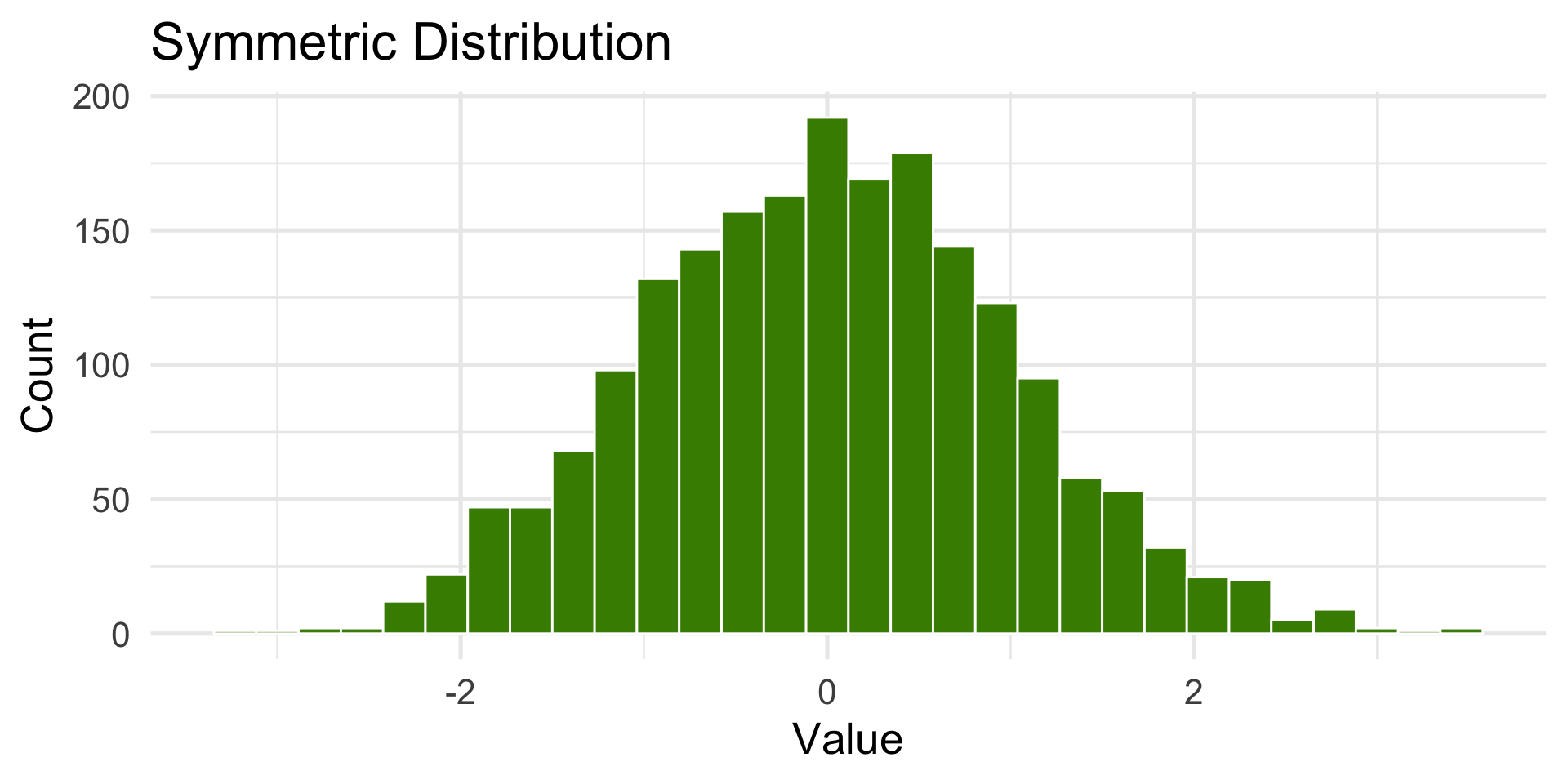
How the Center is measured

How do we find where our data is centered?

Example:

Data: [2, 5, 3, 25, 5]

• The mean is the average of the values. Common measure of central tendency but sensitive to outliers.

  Mean = (2 + 3 + 5 + 5 + 25) / 5 = 8

• The median is the value that separates the higher half from the lower half of the data.

  Ordered Data: [2, 3, 5, 5, 25], Median = 5

Normal Distribution

set.seed(7)
dist <- tibble(x = rnorm(2000, mean = 0, sd = 1))

stats <- dist |> 
  summarize(
    mean_x = mean(x),
    median_x = median(x)
  )

ggplot(dist, aes(x)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white") +
  geom_vline(aes(xintercept = stats$mean_x), color = "red", linewidth = 1) +
  geom_vline(aes(xintercept = stats$median_x), color = "blue", linewidth = 1, linetype = "dashed") +
  labs(
    title = "Normal Distribution (with Mean & Median)",
    x = "Value",
    y = "Count"
  ) +
  annotate("text", x = stats$mean_x + 0.3, y = 200, label = "Mean", color = "red") +
  annotate("text", x = stats$median_x - 0.3, y = 200, label = "Median", color = "blue") + theme_minimal(base_size = 16)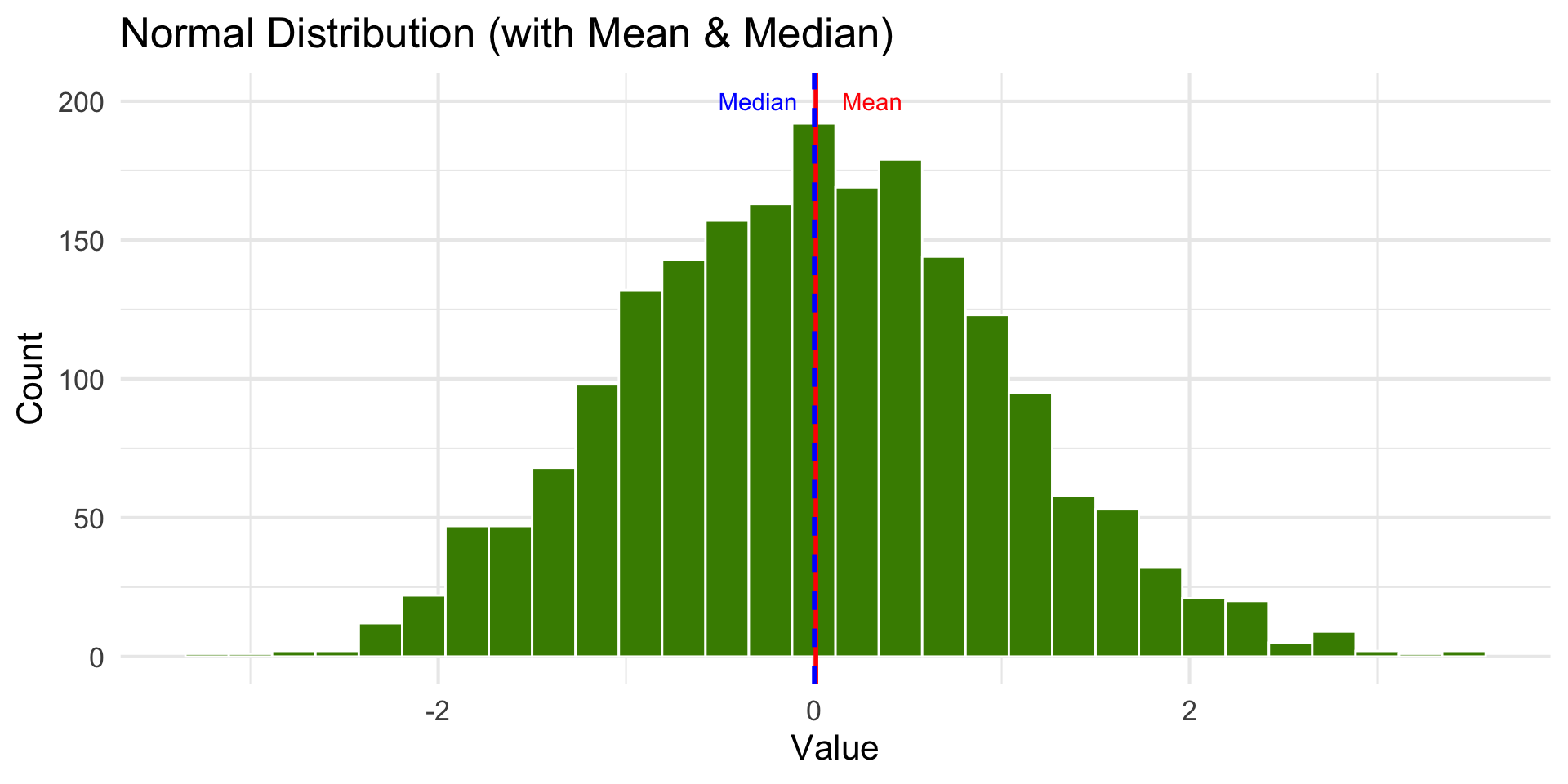

Bimodal Distribution

library(ggplot2)
library(tibble)
library(dplyr)

set.seed(1)
dist <- tibble(x = c(rnorm(10000, mean = -2, sd = 1),
                     rnorm(10000, mean =  3, sd = 1)))

stats <- dist |>
  summarize(
    mean_x   = mean(x),
    median_x = median(x)
  )

ggplot(dist, aes(x)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  geom_vline(aes(xintercept = stats$mean_x),   color = "red",  linewidth = 1) +
  geom_vline(aes(xintercept = stats$median_x), color = "blue", linewidth = 1, linetype = "dashed") +
  labs(title = "Bimodal Distribution (with Mean & Median)",
       x = "Value", y = "Count") +
  annotate("text", x = stats$mean_x + 0.4,  y = 1500, label = "Mean",   color = "red") +
  annotate("text", x = stats$median_x - 0.4,y = 1500, label = "Median", color = "blue") + theme_minimal(base_size = 16)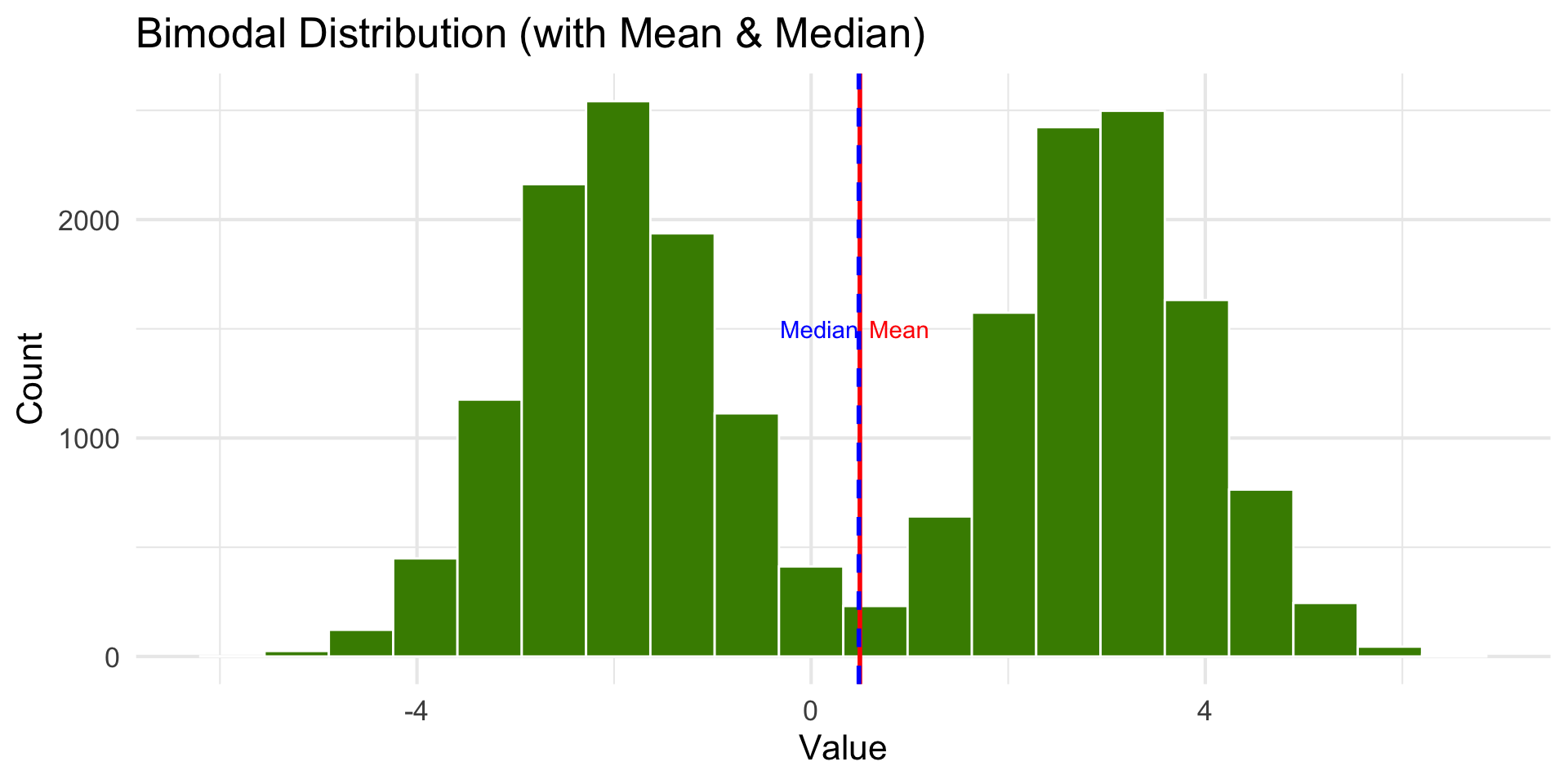

Data like this might be the combination of two groups. Taking the mean is not meaningful until the groups are separated.

Right-Skewed Distribution

dist <- tibble(x = rbeta(10000, 1, 8))
stats <- dist |> 
  summarize(
    mean_x = mean(x),
    median_x = median(x)
  )

ggplot(dist, aes(x)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  geom_vline(aes(xintercept = stats$mean_x), color = "red", linewidth = 1) +
  geom_vline(aes(xintercept = stats$median_x), color = "blue", linewidth = 1, linetype = "dashed") +
  labs(title = "Right-Skewed Distribution", x = "Value", y = "Count") +
  annotate("text", x = stats$mean_x + 0.1, y = 1800, label = "Mean →", color = "red") +
  annotate("text", x = stats$median_x - 0.1, y = 1800, label = "Median", color = "blue") + theme_minimal(base_size = 16)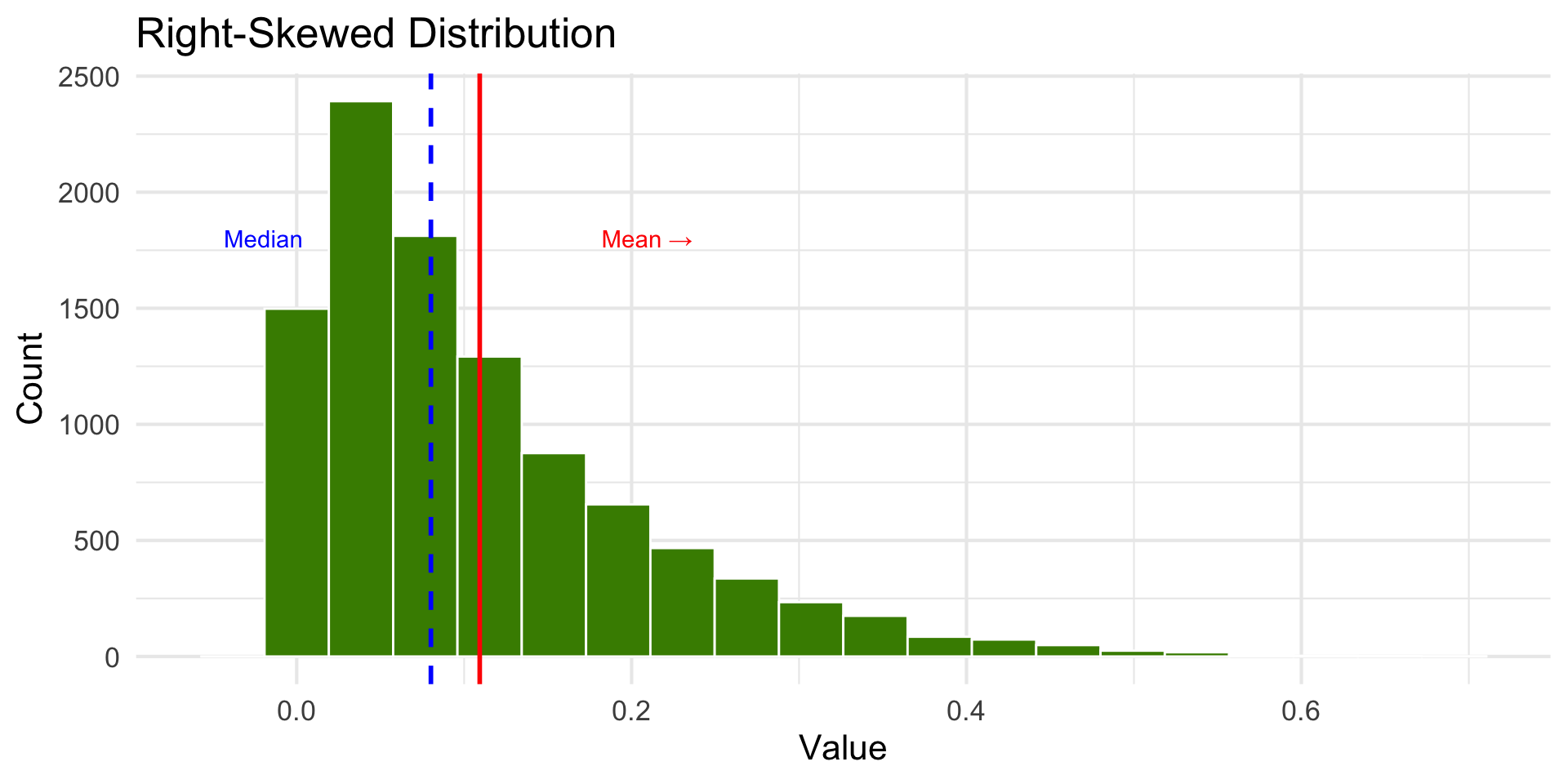

Left-Skewed Distribution

dist <- tibble(x = rbeta(10000, 8, 1))
stats <- dist |> 
  summarize(
    mean_x = mean(x),
    median_x = median(x)
  )

ggplot(dist, aes(x)) +
  geom_histogram(bins = 20, fill = "chartreuse4", color = "white") +
  geom_vline(aes(xintercept = stats$mean_x), color = "red", linewidth = 1) +
  geom_vline(aes(xintercept = stats$median_x), color = "blue", linewidth = 1, linetype = "dashed") +
  labs(title = "Left-Skewed Distribution", x = "Value", y = "Count") +
  annotate("text", x = stats$mean_x - 0.1, y = 1800, label = "Mean ←", color = "red") +
  annotate("text", x = stats$median_x + 0.1, y = 1800, label = "Median", color = "blue")+ theme_minimal(base_size = 16)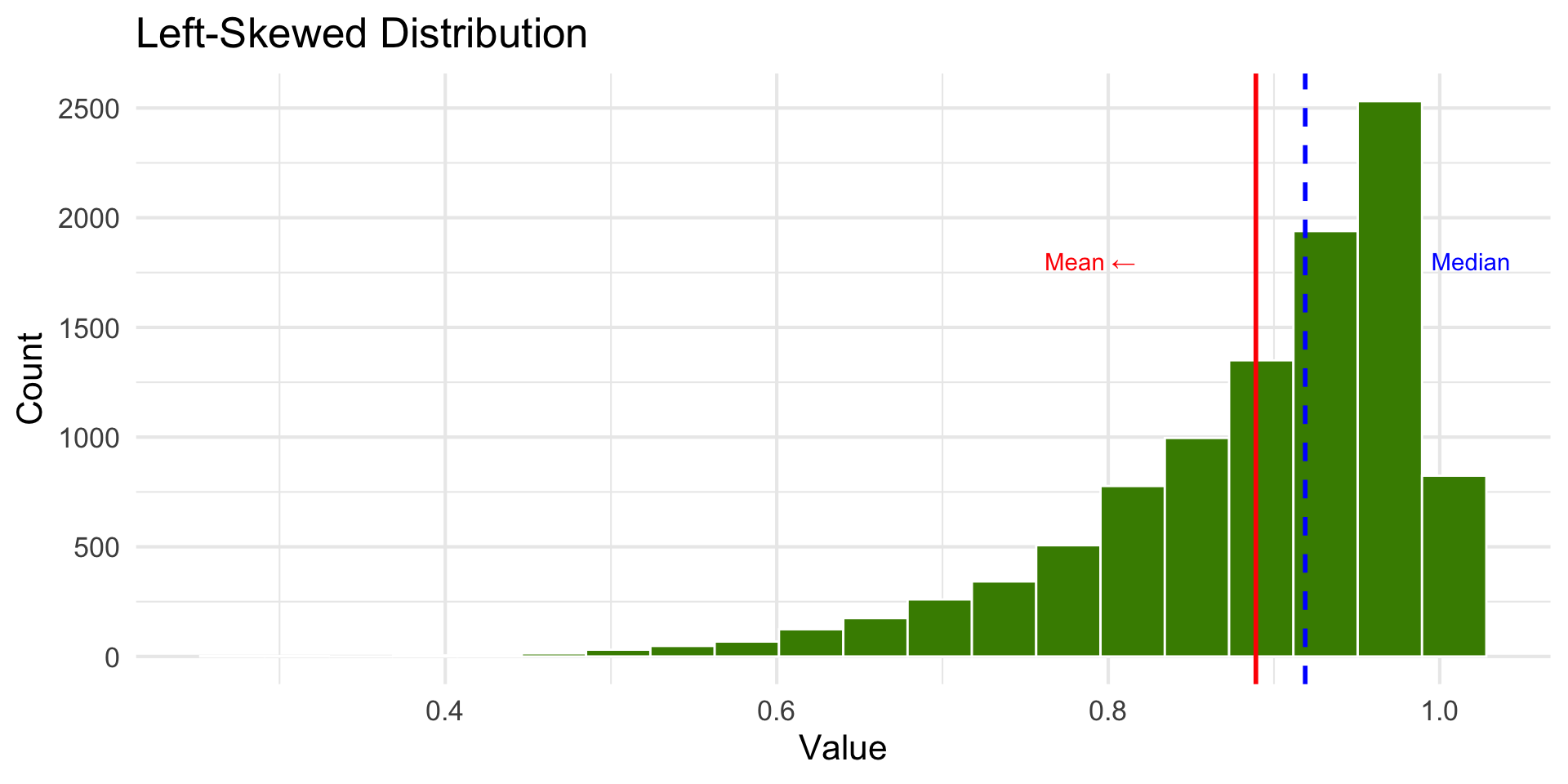

Describing Distribution Shape

• Number of peaks (modes): unimodal, bimodal, multimodal
  
• Direction of skew: left-skewed or right-skewed
  
• Symmetry: is the distribution balanced?
  
• Outliers: extreme values stretching or distorting shape

Summary: Center measurements

• The mean works well as a summary statistic when the distribution is relatively symmetric.
• With skewed distributions, the mean is sensitive to extreme values.
• The median is preferred when data is not symmetric.
• Except when distributions are skewed or bimodal (or multi-modal).
• Bimodal data should be processed by separating into groups based on categories or using clustering.

Measures of Central Tendency

• We can use statistics like mean or median to describe the center of a variable.
• We can visualize the entire distribution to characterize the distribution of the variable.
• We should also say something about the spread of the distribution.

Why Measure and Visualize Spread?

Measures of Spread: Min-Max Range

• maximum (max())
• minimum (min())
• range (max - min values)

Good to know but not any insight about the distribution or if there are outliers.

penguins |>
  drop_na(body_mass_g) |>
  summarize(
    min_mass    = min(body_mass_g),
    max_mass    = max(body_mass_g),
    range_mass  = max(body_mass_g) - min(body_mass_g),
  )

# A tibble: 1 × 3
  min_mass max_mass range_mass
     <int>    <int>      <int>
1     2700     6300       3600

Measures of Spread: IQR

How do we find where most of the data lie?

Example:

Data: [12, 5, 2, 4, 7, 15, 8, 10]

Measures of Spread: IQR

Quantiles split the ordered data into equal parts.

Ordered Data: [2, 4, 5, 7, 8, 10, 12, 15]

• Q1 (25th percentile): 4.5 (between 4 and 5)
  
• Q2 (50th percentile / Median): 7.5 (between 7 and 8)
  
• Q3 (75th percentile): 11 (between 10 and 12)

Measures of Spread: IQR

The Interquartile Range (IQR) measures the spread of the middle 50% of data.

\[\text{IQR} = Q3 - Q1 = 11 - 4.5 = 6.5\]

The IQR tells us where the central half of the data lie —
it’s a robust measure of spread as it ignores extreme values like the min and max.

Measures of Spread: IQR

penguins |>
  drop_na(body_mass_g) |>
  summarize(
    q1_mass     = quantile(body_mass_g, 0.25),
    median_mass = median(body_mass_g),
    q3_mass     = quantile(body_mass_g, 0.75),
    iqr_mass    = IQR(body_mass_g)
  )

# A tibble: 1 × 4
  q1_mass median_mass q3_mass iqr_mass
    <dbl>       <dbl>   <dbl>    <dbl>
1    3550        4050    4750     1200

Box Plot

• A box plot is a graphical representation of the distribution based on the median and quartiles.
• It is a standardized way of displaying the distribution of data based on a five number summary: minimum, first quartile, median, third quartile, and maximum.

library(palmerpenguins)
library(ggplot2)

ggplot(penguins, aes(x = "", y = body_mass_g)) +
  geom_boxplot(fill = "chartreuse4") +
  labs(
    x = "",
    y = "Body Mass (g)",
    title = "Distribution of Penguin Body Mass",
    caption = "Source: palmerpenguins"
  ) +
  theme_minimal(base_size = 20)

How Outliers Affect Spread

Example:

Data: [2, 4, 5, 7, 8, 10, 12, 15, 50]

• Q1 (25th percentile): 5
  
• Q2 (Median): 8
  
• Q3 (75th percentile): 12
• \[ \begin{aligned} \text{IQR} &= Q3 - Q1 = 12 - 5 = 7 \end{aligned} \]

How Outliers Affect Spread

Example:

Data: [2, 4, 5, 7, 8, 10, 12, 15, 50]

• The min-max range changes a lot: \(50 - 2 = 48\)
• The IQR stays nearly the same (from 6.5 to 7).
  
• The IQR is robust (it ignores the extreme outlier).

Boxplot with Outlier

Example:
Data: [2, 4, 5, 7, 8, 10, 12, 15, 50]

Whiskers extend extend up to \(1.5 \times IQR\) beyond the box. Anything farther out is flagged as an outlier and plotted as a red point.

Boxplot with Outlier

library(ggplot2)
library(tibble)

data <- tibble(x = c(2, 4, 5, 7, 8, 10, 12, 15, 50))

ggplot(data, aes(x = "", y = x)) +
  geom_boxplot(fill = "chartreuse4", color = "black", outlier.color = "red", outlier.shape = 19, width = 0.3) +
  labs(
    title = "Boxplot with Outlier",
    x = "",
    y = "Value"
  ) +
  theme_minimal(base_size = 20)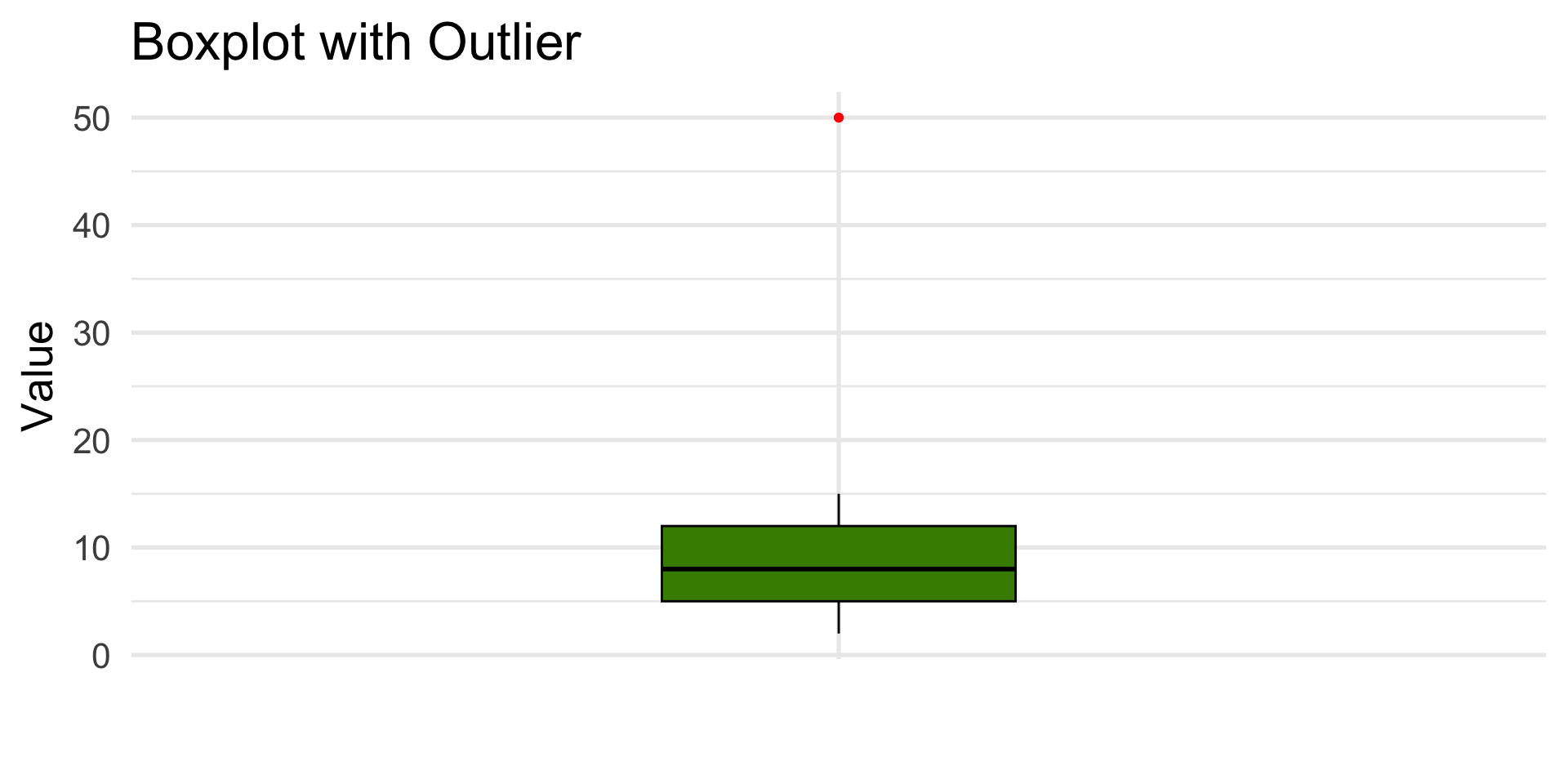

Measures of Spread

penguins |>
  drop_na(body_mass_g) |>
  summarize(
    mean_mass   = mean(body_mass_g),
    median_mass = median(body_mass_g),
    q25_mass    = quantile(body_mass_g, 0.25),
    q75_mass    = quantile(body_mass_g, 0.75),
    sd_mass     = sd(body_mass_g),
    iqr_mass    = IQR(body_mass_g),
    min_mass    = min(body_mass_g),
    max_mass    = max(body_mass_g),
    range_mass  = max(body_mass_g) - min(body_mass_g),
    n_obs       = n()
  )

# A tibble: 1 × 10
  mean_mass median_mass q25_mass q75_mass sd_mass iqr_mass min_mass max_mass
      <dbl>       <dbl>    <dbl>    <dbl>   <dbl>    <dbl>    <int>    <int>
1     4202.        4050     3550     4750    802.     1200     2700     6300
# ℹ 2 more variables: range_mass <int>, n_obs <int>

More measures of Spread: Standard Deviation and Variance

Next lecture