Measuring Distributions

Sarah Cassie Burnett

October 16, 2025

Recap: Describing a Distribution

When summarizing a dataset, report all four key features:

Center — e.g., mean or median
Spread — e.g., IQR or standard deviation
Shape — e.g., skewness, modality (unimodal, bimodal)
Unusual points — e.g., outliers or extreme values

Recap: Describing Distributions

Last time, we focused on two main features of a distribution:

Center — the typical value (mean or median)
Spread — how far values vary from that center

Together, these give a complete summary of a dataset’s pattern.

Center: Mean vs. Median

Mean works well when data is symmetric and not affected by outliers.
Median is robust — it’s better when the data are skewed or have extreme values.
For bimodal or multimodal data,
- your data could need to be separated into groups first, or
- your data could be under sampled.

Undersampled vs. Well-sampled

Let’s look at penguin flipper length.
Here’s a histogram across three species:

Code

library(tidyverse)
library(palmerpenguins)
ggplot(penguins, aes(x = flipper_length_mm)) +
  geom_histogram(fill = "chartreuse4", color = "white", bins = 12, alpha = 0.8) +
  labs(
    title = "All penguins",
    x = "Flipper Length (mm)",
    y = "Count"
  ) +
  theme_minimal(base_size = 16)

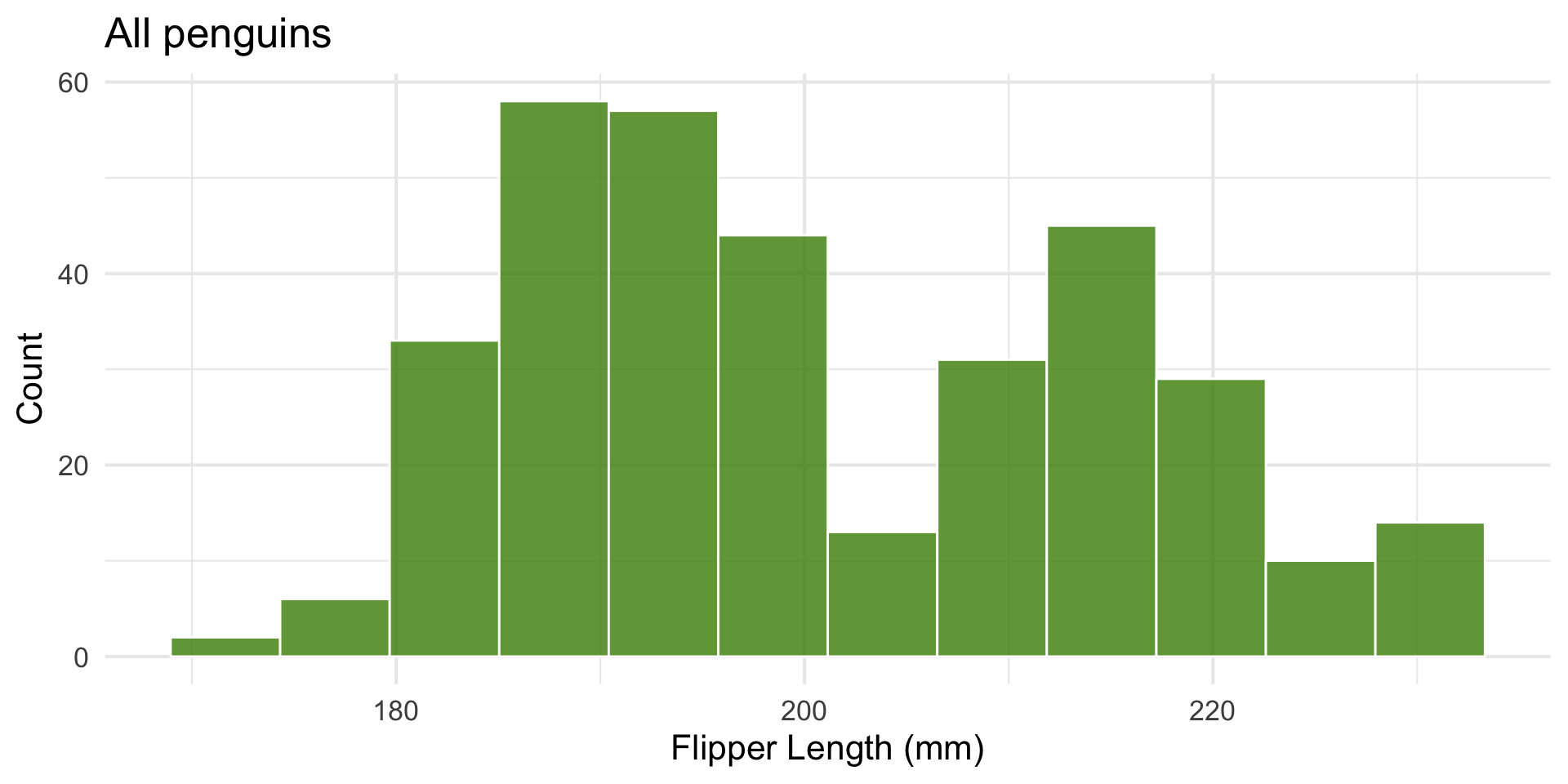
Look at one group’s distribution

Let’s look at penguin flipper length.
Filter for only ‘Adelie’.

Code

library(tidyverse)
library(palmerpenguins)
set.seed(7)

Adelie_penguins <- penguins |> filter(species == "Adelie") 

ggplot(Adelie_penguins, aes(x = flipper_length_mm)) +
  geom_histogram(fill = "chartreuse4", color = "white", bins = 12, alpha = 0.8) +
  labs(
    title = "151 Adelie penguins",
    x = "Flipper Length (mm)",
    y = "Count") + theme_minimal(base_size = 16)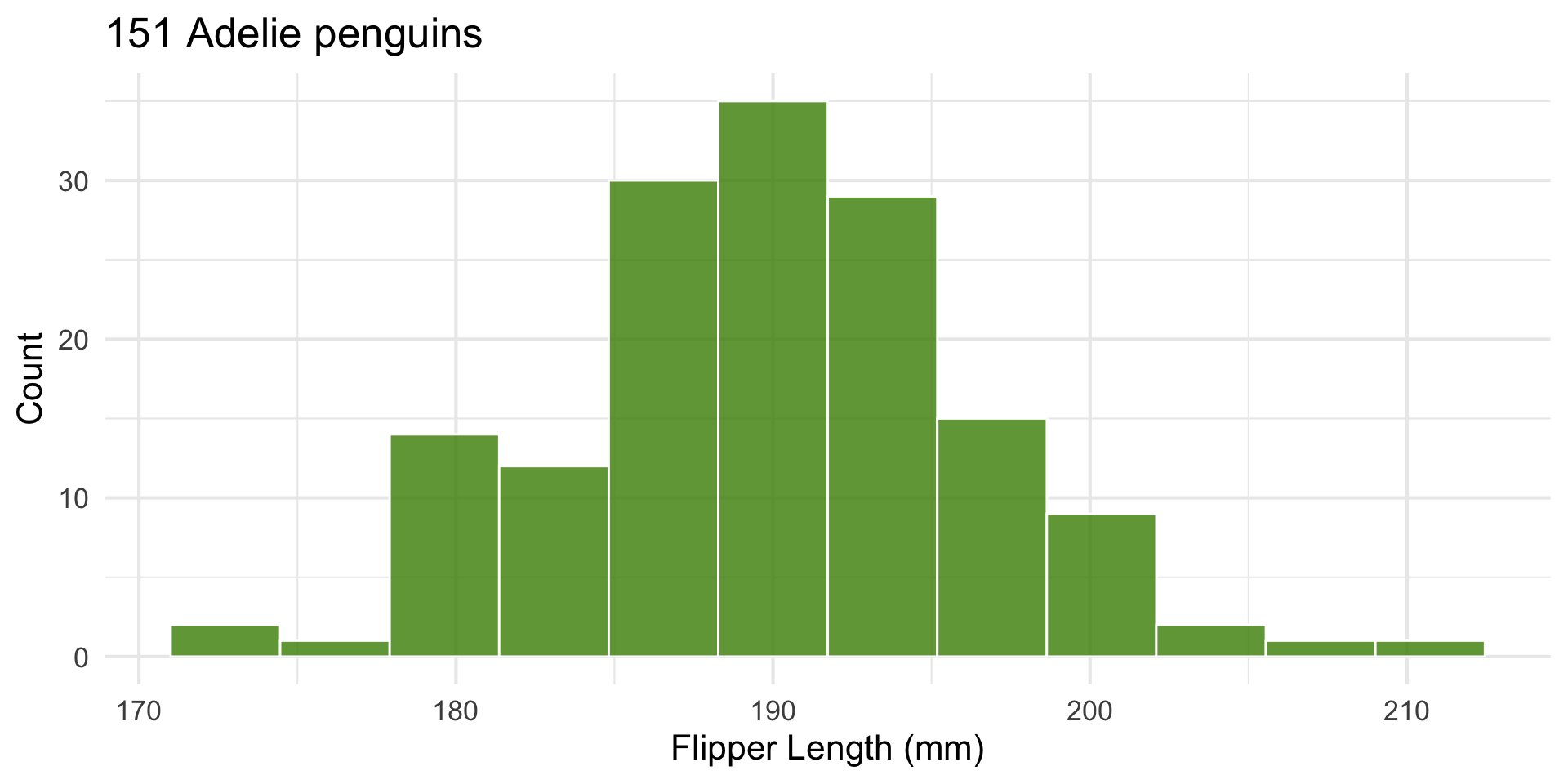

Undersampled vs. Well-sampled

Let’s look at penguin flipper length.
We’ll compare a tiny random sample to a large one.

Code

library(tidyverse)
library(palmerpenguins)
set.seed(7)


Adelie_penguins <- penguins |> 
  filter(species == "Adelie") |> 
  drop_na(flipper_length_mm)

# Undersampled (n = 10)
small_sample <- Adelie_penguins |> 
  sample_n(10)

Code

# Plot side by side
p_small <- ggplot(small_sample, aes(x = flipper_length_mm)) +
  geom_histogram(fill = "chartreuse4", color = "white", bins = 8, alpha = 0.8) +
  labs(
    title = "Undersampled (n = 10)",
    x = "Flipper Length (mm)",
    y = "Count"
  ) +
  theme_minimal(base_size = 16)

p_large <- ggplot(Adelie_penguins, aes(x = flipper_length_mm)) +
  geom_histogram(fill = "chartreuse4", color = "white", bins = 12, alpha = 0.8) +
  labs(
    title = "151 Adelie penguins",
    x = "Flipper Length (mm)",
    y = "Count"
  ) +
  theme_minimal(base_size = 16)

# Combine later with patchwork:
library(patchwork)
p_small + p_large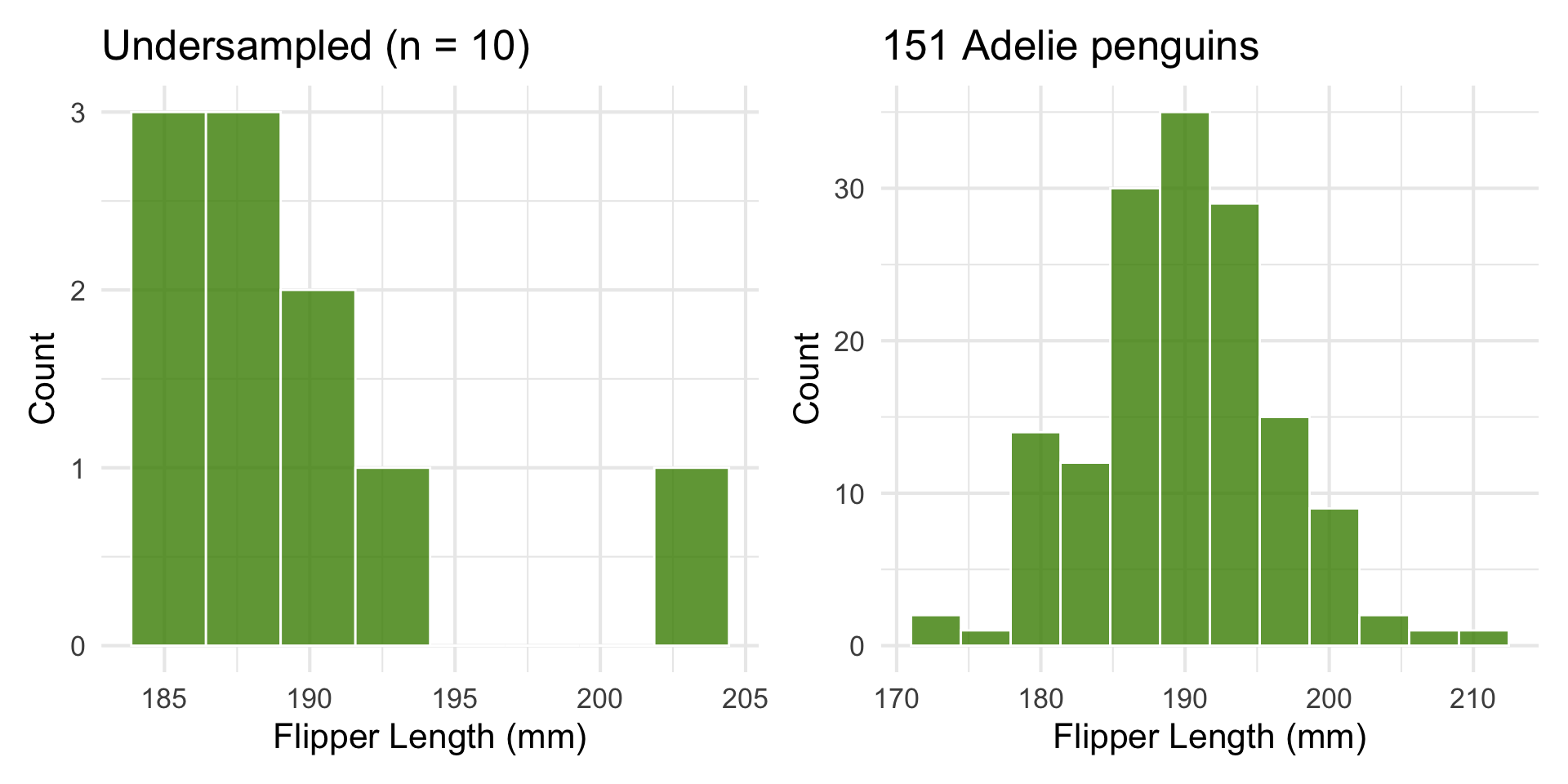

Why Measure Spread?

Two datasets can have the same center but very different variability.
We measure spread to understand how values differ from one another.

Common measures of spread so far:

Range: max − min
IQR (Interquartile Range): spread of the middle 50% of data

Range vs. IQR

Measure	Description	Robust to Outliers?
Range	Distance from minimum to maximum	NO
IQR	Spread of the middle 50% of values	YES

The IQR doesn’t change much even if the dataset has extreme values.

Example: IQR

We’ll use this data:

5, 9, 11, 14, 18, 21, 22

Find the median (Q2)

There are 7 observations (odd number).
Median = 14

Example: IQR

Data: 5, 9, 11, 14, 18, 21, 22

Split the data. In the inclusive method, we include the median in both halves.
- Lower half is 5, 9, 11, 14
- Upper half is 14, 18, 21, 22
Find Q1 and Q3
- Q1 = median of lower half = (9 + 11)/2 = 10
- Q3 = median of upper half = (18 + 21)/2 = 19.5
Compute the \(IQR = Q3 - Q1 = 19.5 - 10 = 9.5\)

Example: IQR

Why “inclusive” method?

We include the median in both halves so that each half represents half of the data up to and including the center.

This is the default method in R, Excel, and Google Sheets.

Summary

library(tidyverse)
data <- tibble(x = c(5, 9, 11, 14, 18, 21, 22))

# Summary of quartiles, IQR, range, etc.
data |>
  summarize(
    min_x  = min(x),
    q1_x   = quantile(x, 0.25),
    median = median(x),
    q3_x   = quantile(x, 0.75),
    max_x  = max(x),
    iqr_x  = IQR(x),
  )

# A tibble: 1 × 6
  min_x  q1_x median  q3_x max_x iqr_x
  <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>
1     5    10     14  19.5    22   9.5

Boxplot

ggplot(data, aes(y = x)) +
  geom_boxplot(fill = "chartreuse4", color = "black", width = 0.3) +
  labs(title = "Boxplot of Data: 5, 9, 11, 14, 18, 21, 22", y = "Value") +
  theme_minimal(base_size = 18)

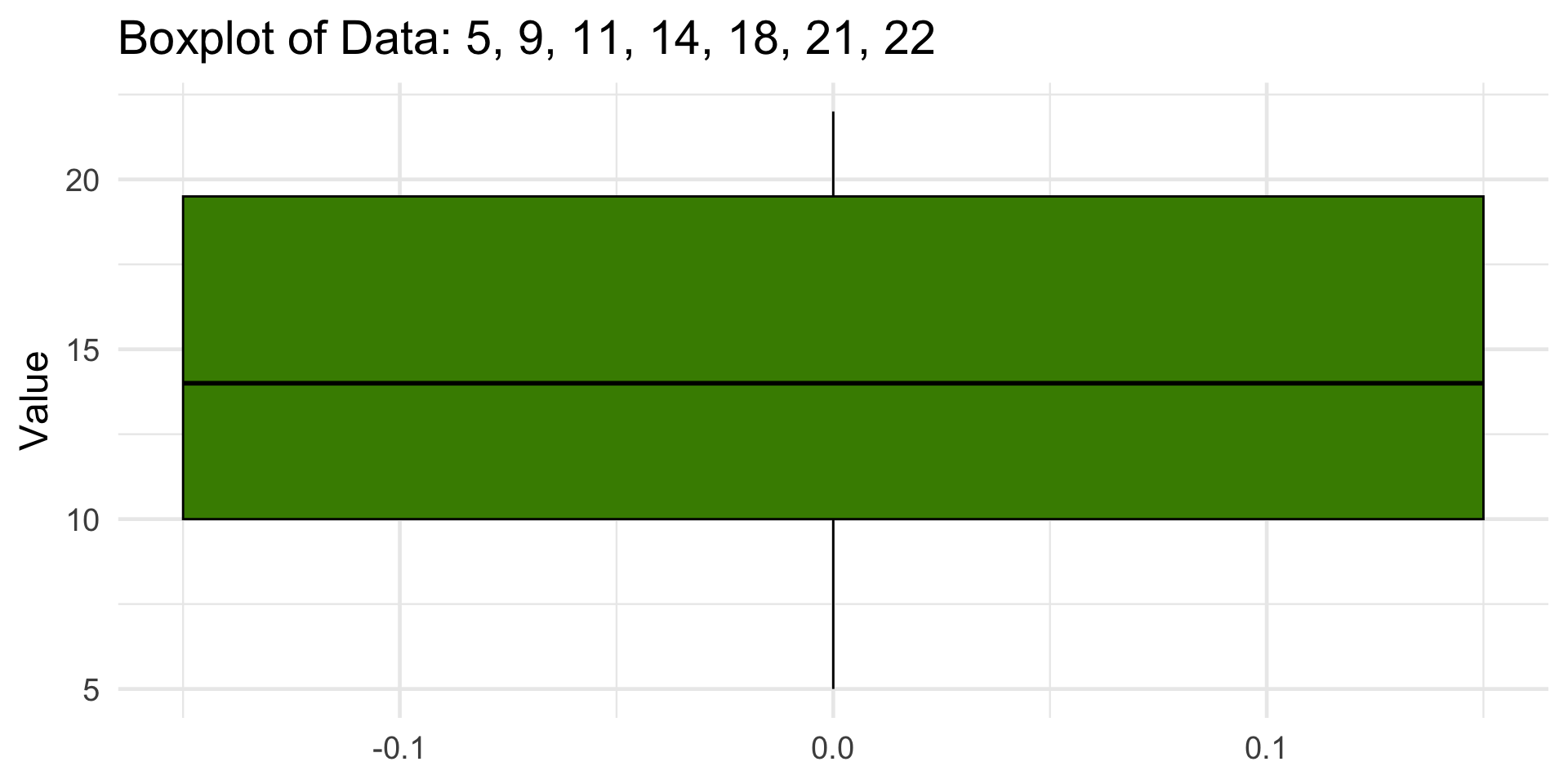
Example: Fences and Outliers

Let’s continue with the same data:

5, 9, 11, 14, 18, 21, 22

We already found that: Q1 = 10, Q3 = 19.5, IQR = 9.5
Compute the fences using the 1.5×IQR rule:

\[\text{Lower Fence} = Q1 - 1.5 \times IQR = 10 - 1.5(9.5) = -4.25\] \[\text{Upper Fence} = Q3 + 1.5 \times IQR = 19.5 + 1.5(9.5) = 33.75\]

Any data values below -4.25 or above 33.75 would be considered outliers.

Check in R

library(tidyverse)
data <- tibble(x = c(5, 9, 11, 14, 18, 21, 22))

data |>
  summarize(
    min_x  = min(x),
    q1_x   = quantile(x, 0.25),
    median = median(x),
    q3_x   = quantile(x, 0.75),
    max_x  = max(x),
    iqr_x  = IQR(x),
    lower_fence = q1_x - 1.5 * iqr_x,
    upper_fence = q3_x + 1.5 * iqr_x
  )

# A tibble: 1 × 8
  min_x  q1_x median  q3_x max_x iqr_x lower_fence upper_fence
  <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>       <dbl>       <dbl>
1     5    10     14  19.5    22   9.5       -4.25        33.8

Visualizing Outliers

Code

library(ggplot2)

ggplot(data, aes(y = x)) +
  geom_boxplot(fill = "chartreuse4", color = "black", width = 0.3, outlier.color = "red", outlier.shape = 19) +
  labs(
    title = "Boxplot of Data with Fences and Potential Outliers",
    y = "Value"
  ) +
  theme_minimal(base_size = 18)

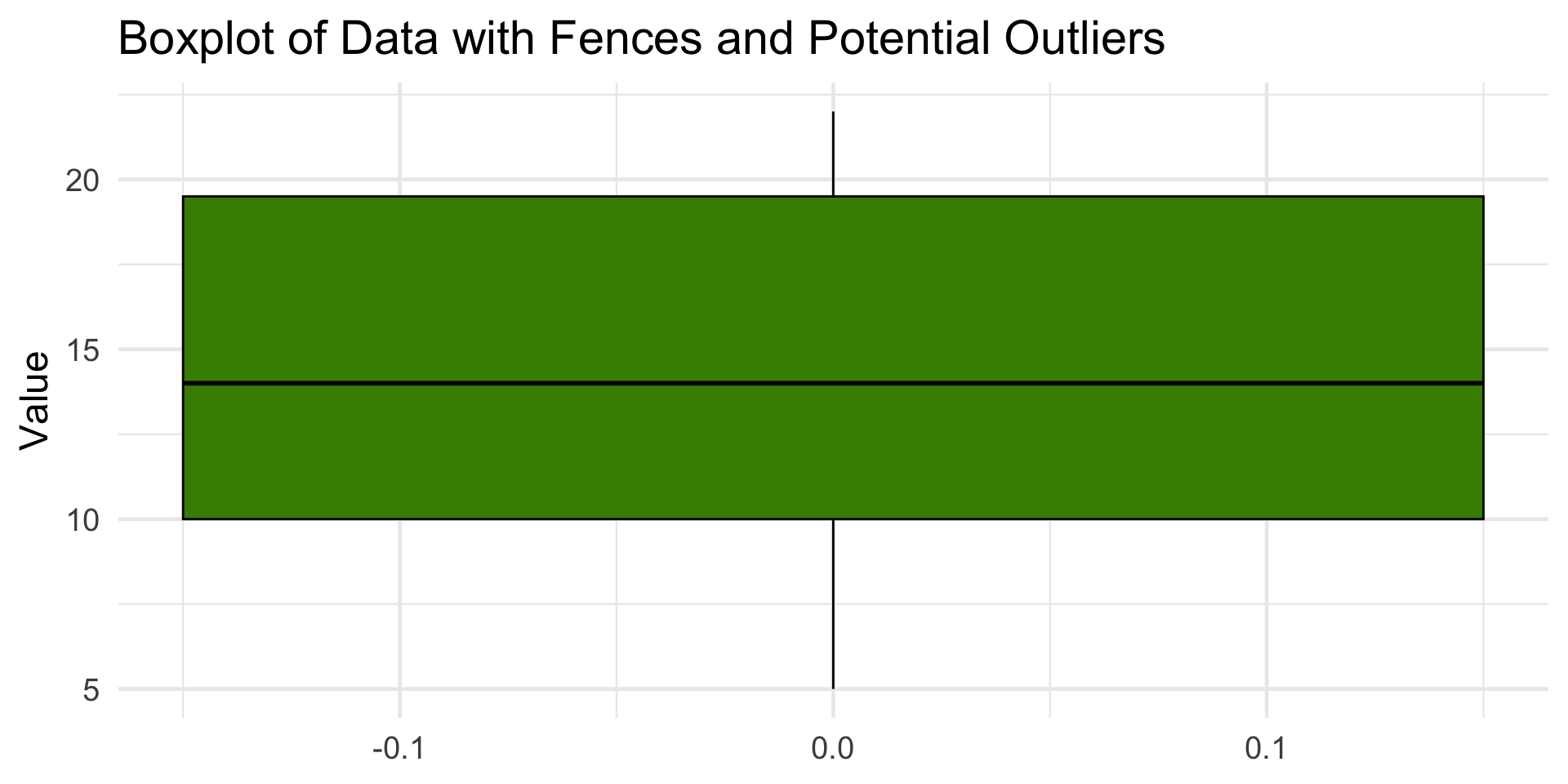
This dataset has no outliers, since all points fall between the fences (–4.25, 33.75).

Boxplots good for comparing distributions across categories

Code

library(palmerpenguins)
ggplot(penguins, aes(x = species, y = body_mass_g)) +
  geom_boxplot(fill = "chartreuse4", outlier.color = "red") +
  labs(
    x = "Species",
    y = "Body Mass (g)",
    title = "Distribution of Penguin Body Mass",
    caption = "Source: palmerpenguins"
  ) +
  theme_minimal(base_size = 20)

Try it out! Compute and Visualize by Hand

Dataset: 10, 2, 25, 8, 6, 12, 4

Pair up and compute the following by hand:

Median
Q1 and Q3
Interquartile Range (IQR = Q3 − Q1)
Lower and Upper Fences (1.5×IQR rule)
Identify any potential outliers

Then sketch a rough boxplot of the data.

05:00

Check with R

data <- tibble(x = c(10, 2, 25, 8, 6, 12, 4))

data |> 
  summarize(
    min_x  = min(x),
    q1_x   = quantile(x, 0.25),
    median = median(x),
    q3_x   = quantile(x, 0.75),
    max_x  = max(x),
    iqr_x  = IQR(x),
    lower_fence = q1_x - 1.5 * iqr_x,
    upper_fence = q3_x + 1.5 * iqr_x
  )

# A tibble: 1 × 8
  min_x  q1_x median  q3_x max_x iqr_x lower_fence upper_fence
  <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>       <dbl>       <dbl>
1     2     5      8    11    25     6          -4          20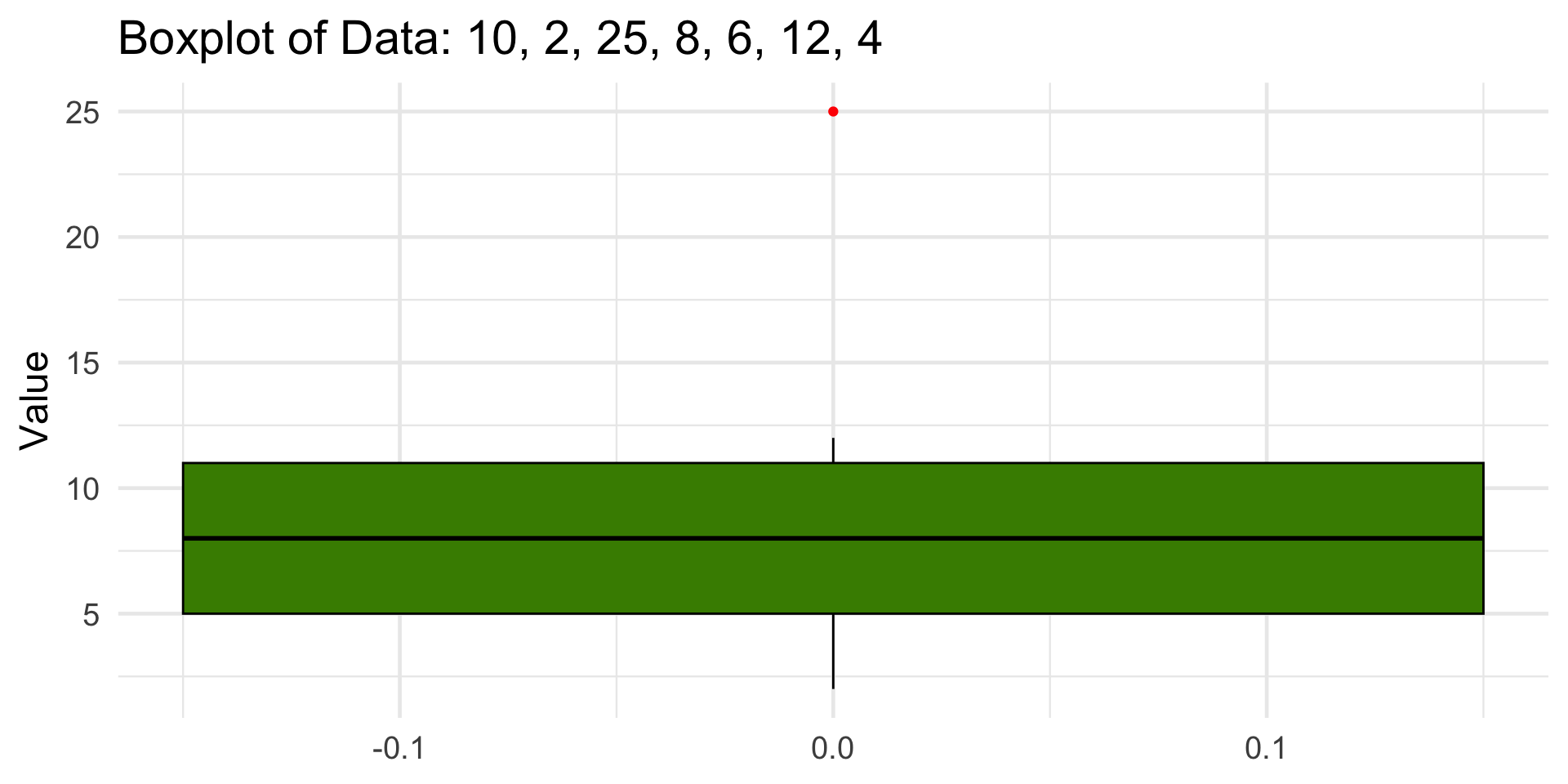

Code

library(ggplot2)

ggplot(data, aes(y = x)) +
  geom_boxplot(fill = "chartreuse4", color = "black", width = 0.3, outlier.color = "red") +
  labs(
    title = "Boxplot of Data: 10, 2, 25, 8, 6, 12, 4",
    y = "Value"
  ) +
  theme_minimal(base_size = 18)

Variance and Standard Deviation

Variance and standard deviation measure how far values spread around the mean.

Variance

The variance (sample variance) is the average squared distance from the mean.

\[ \sigma^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1} \]

Where:

\(x_i\) — an individual data point

\(\bar{x}\) — the sample mean (average of all data points)

\(n\) — the number of observations in the sample

\(\sigma^2\) — the sample variance (a measure of spread)

\((x_i - \bar{x})\) — the deviation of each observation from the mean

Variance increases when data points are farther from the mean — it reflects how “spread out” the dataset is overall.

Standard Deviation

The standard deviation (SD) is the square root of the variance.
It’s in the same units as the data.

\[ \sigma = \sqrt{\sigma^2} \]

Standard Deviation

A low standard deviation indicates that the values tend to be close to the mean
A high standard deviation indicates that the values are spread out over a wider range

Calculating Deviation from the Mean

First, calculate the mean (\(\bar{x}\)) of the dataset.
For each data point (\(x_i\)), calculate its deviation from the mean: \[x_i - \bar{x}\]

Square the Deviations

Square each deviation to eliminate negative values: \[(x_i - \bar{x})^2\]
Sum up all squared deviations: \[\sum_{i=1}^{n} (x_i - \bar{x})^2\]
This sum represents the total squared deviation from the mean.

Calculating the Variance

Divide the total squared deviation by \((n-1)\) (to account for the sample variance): \[\sigma^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2\]
Using \((n-1)\) ensures an unbiased estimate of the population variance when calculating from a sample.

Deriving the Standard Deviation

The standard deviation is the square root of the variance: \[\sigma = \sqrt{\sigma^2}\]
Taking the square root converts the variance back to the units of the original data.

Example: Variance and SD by Hand

Data: 2, 4, 6, 8

Mean = (2 + 4 + 6 + 8) / 4 = 5
Compute each deviation:
\[ x_i - \bar{x} = \begin{cases} 2 - 5 = -3 \\ 4 - 5 = -1 \\ 6 - 5 = +1 \\ 8 - 5 = +3 \end{cases} \]

Example: Variance and SD by Hand

Data: 2, 4, 6, 8

Deviations: −3, −1, +1, +3
Square each deviation to remove negatives:

\[ (x_i - \bar{x})^2 = \begin{cases} (-3)^2 = 9 \\ (-1)^2 = 1 \\ (+1)^2 = 1 \\ (+3)^2 = 9 \end{cases} \]

Example: Variance and SD by Hand

Data: 2, 4, 6, 8

Squared deviations: 9, 1, 1, 9
Variance: \(\sigma^2 = \frac{9 + 1 + 1 + 9}{4 - 1} = \frac{20}{3} \approx 6.7\)
Standard deviation: \(\sigma = \sqrt{6.7} \approx 2.6\)

Standard Deviation Calculation in R

x <- c(2, 4, 6, 8)
spread <- x - mean(x)
spread

[1] -3 -1  1  3

Standard Deviation Calculation in R

x <- c(2, 4, 6, 8)
spread_squared <- spread^2
spread_squared

[1] 9 1 1 9

Standard Deviation Calculation in R

x <- c(2, 4, 6, 8)
sum_spread_squared <- sum(spread_squared)
sum_spread_squared

[1] 20

Standard Deviation Calculation in R

n <- length(x)
variance <- sum_spread_squared/(n-1)
variance

[1] 6.666667

Standard Deviation Calculation in R

standard_dev <- sqrt(variance)
standard_dev

[1] 2.581989

sd(x)

[1] 2.581989

Interpreting SD

Small SD means data are tightly clustered around the mean
Large SD means data are spread out
Units: always the same as the data itself (e.g., cm, dollars, points)

Visual Comparison

Code

library(patchwork)
x <- tibble(x = rnorm(1000, mean = 0, 2))
a <- ggplot(x, aes(x = x )) +
  geom_histogram(binwidth = .5, fill = "chartreuse4") + theme_bw(base_size = 14) +
  geom_vline(xintercept = mean(x$x), color = "red", linewidth = 1) +
  geom_vline(xintercept = mean(x$x) - sd(x$x), color = "blue", linetype = "dashed") +
  geom_vline(xintercept = mean(x$x) + sd(x$x), color = "blue", linetype = "dashed") +
   labs(
    x = "Value", 
    y = "Count", 
    title = "A Distribution with Mean = 0, SD = 2"
  ) + xlim(-20, 20)
x <- tibble(x = rnorm(1000,mean = 0, 10))
b <- ggplot(x, aes(x = x )) +
  geom_histogram(binwidth = .5, fill = "chartreuse4") + theme_bw(base_size = 14) +
  geom_vline(xintercept = mean(x$x), color = "red", linewidth = 1) +
  geom_vline(xintercept = mean(x$x) - sd(x$x), color = "blue", linetype = "dashed") +
  geom_vline(xintercept = mean(x$x) + sd(x$x), color = "blue", linetype = "dashed") +
   labs(
    x = "Value", 
    y = "Count", 
    title = "A Distribution with Mean = 0, SD = 10"
  ) + xlim(-20, 20)
a + b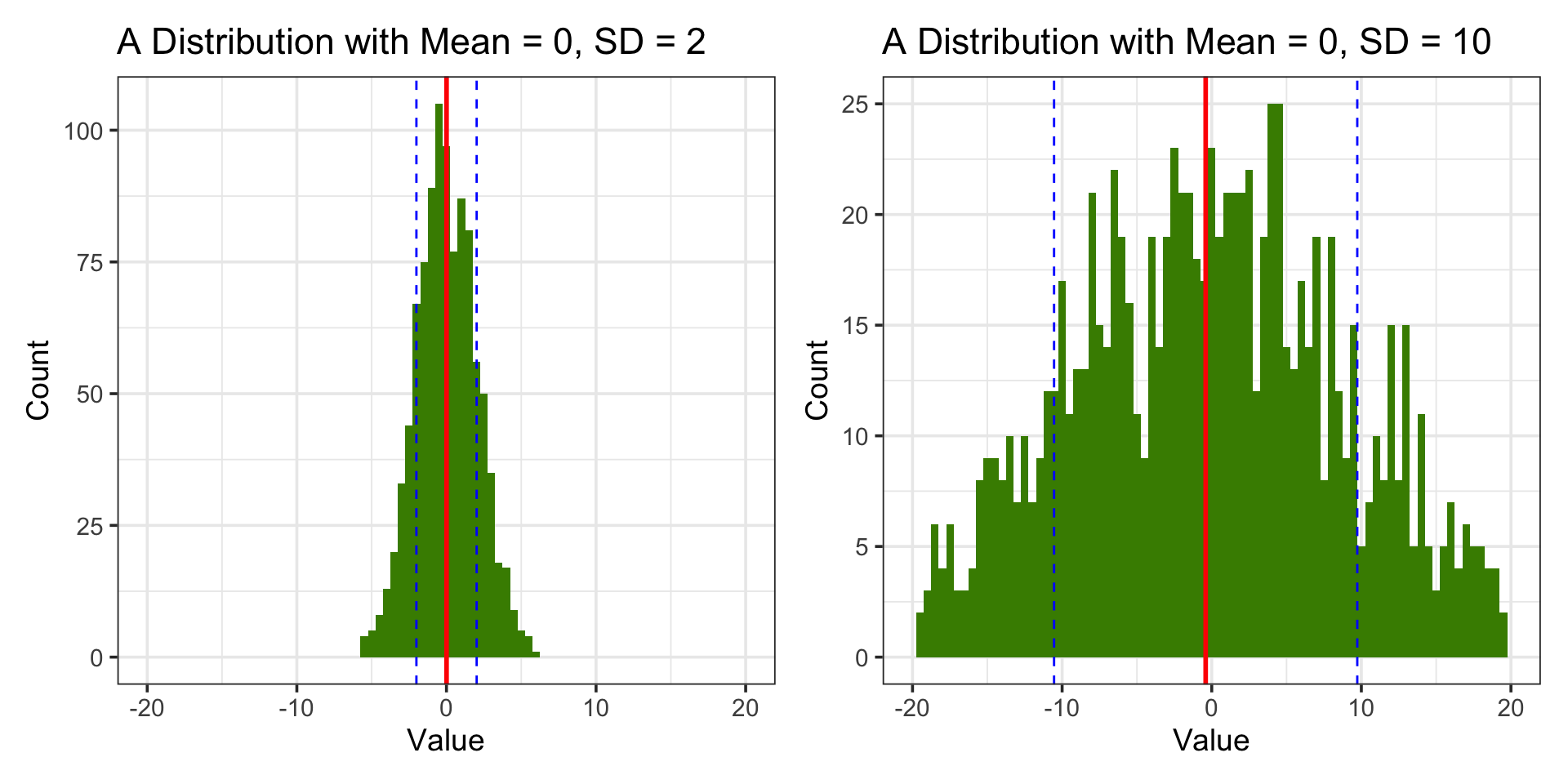

Summary

Measure	What it Describes	Units	Robust to Outliers?
Range	Entire spread	Same as data	NO
IQR	Middle 50% of data	Same as data	YES
Variance	Average squared distance	Squared units	NO
Standard Deviation	Typical distance from mean	Same as data	NO

Z-Scores

A z-score tells how many standard deviations a value \(x\) is from the mean.

\[ z = \frac{x - \bar{x}}{\sigma} \]

Positive is above the mean
Negative is below the mean
Values with \(|z| > 2\) are often considered unusual

Example: Calculating Z-Scores

Dataset: 2, 4, 6, 8
Mean = 5, SD ≈ 2.6

x	z-score	Interpretation
2	(2−5)/2.6 ≈ −1.15	below average
4	(4−5)/2.6 ≈ −0.38	slightly below
6	(6−5)/2.6 ≈ +0.38	slightly above
8	(8−5)/2.6 ≈ +1.15	above average

Compute in R

x <- c(2, 4, 6, 8)
z <- (x - mean(x)) / sd(x)

# Display both values and z-scores
tibble(Value = x, Z_Score = round(z, 2))

# A tibble: 4 × 2
  Value Z_Score
  <dbl>   <dbl>
1     2   -1.16
2     4   -0.39
3     6    0.39
4     8    1.16

Interpreting Z-Scores

A z-score of 0 means the value equals the mean.
A z-score of +1 means 1 SD above the mean.
A z-score of −1 means 1 SD below the mean.
Extreme z-scores (e.g., beyond ±2 or ±3) may indicate outliers or rare events.

Visual Example

Code

library(ggplot2)
set.seed(7)
data <- tibble(x = rnorm(500, mean = 0, sd = 4))

mean_x <- mean(data$x)
sd_x <- sd(data$x)

ggplot(data, aes(x)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white", alpha = 0.8) +
  geom_vline(xintercept = mean_x, color = "red", linewidth = 1) +
  geom_vline(xintercept = mean_x + c(-1, 1) * sd_x, color = "blue", linetype = "dashed") +
  geom_vline(xintercept = mean_x + c(-2, 2) * sd_x, color = "purple", linetype = "dotted") +
  labs(
    title = "Standard Normal Distribution with Z-Scores",
    x = "Value",
    y = "Count"
  ) +
  theme_minimal(base_size = 18) + annotate("text", x = mean_x -1.3, y = 40, label = "Mean (z = 0)", color = "red", vjust = -0.5) +
  annotate("text", x = mean_x + sd_x -.7 , y = 40, label = "z = +1", color = "blue", vjust = -0.5) +
  annotate("text", x = mean_x - sd_x -.7, y = 40, label = "z = -1", color = "blue", vjust = -0.5) +
  annotate("text", x = mean_x + 2 * sd_x -.7, y = 40, label = "z = +2", color = "purple", vjust = -0.5) +
  annotate("text", x = mean_x - 2 * sd_x - .7, y = 40, label = "z = -2", color = "purple", vjust = -0.5)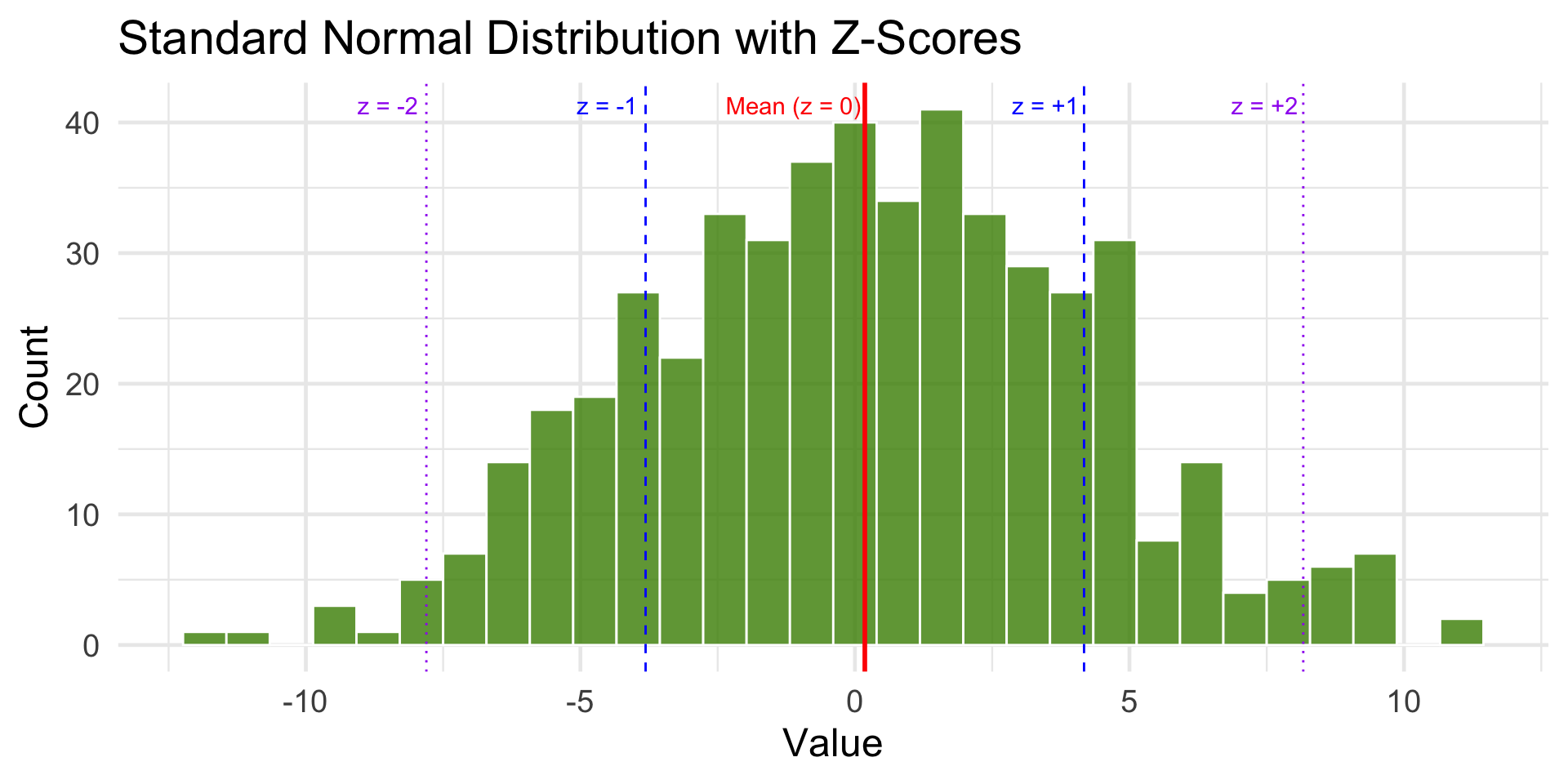

Visual Example: Z-score vs. IQR

Code

library(ggplot2)
library(dplyr)

set.seed(7)
data <- tibble(x = rnorm(500, mean = 0, sd = 4))

# Mean and standard deviation (for z-scores)
mean_x <- mean(data$x)
sd_x <- sd(data$x)

# Median and IQR (for fences)
Q1 <- quantile(data$x, 0.25)
Q3 <- quantile(data$x, 0.75)
IQR_val <- IQR(data$x)
lower_fence <- Q1 - 1.5 * IQR_val
upper_fence <- Q3 + 1.5 * IQR_val

ggplot(data, aes(x)) +
  geom_histogram(bins = 30, fill = "chartreuse4", color = "white", alpha = 0.8) +
  
  # Mean and z-score lines
  geom_vline(xintercept = mean_x, color = "red", linewidth = 1) +
  geom_vline(xintercept = mean_x + c(-1, 1) * sd_x, color = "blue", linetype = "dashed") +
  geom_vline(xintercept = mean_x + c(-2, 2) * sd_x, color = "purple", linetype = "dotted") +
  
  # IQR and fence lines
  geom_vline(xintercept = c(Q1, Q3), color = "orange", linetype = "solid", linewidth = 1) +
  geom_vline(xintercept = c(lower_fence, upper_fence), color = "brown", linetype = "dashed") +
  
  labs(
    title = "Comparing Z-Scores and IQR Fences",
    x = "Value",
    y = "Count"
  ) +
  theme_minimal(base_size = 18) +

  # Z-score annotations
  annotate("text", x = mean_x -1.3, y = 40, label = "Mean (z = 0)", color = "red", vjust = -0.5) +
  annotate("text", x = mean_x + sd_x - .7 , y = 40, label = "z = +1", color = "blue", vjust = -0.5) +
  annotate("text", x = mean_x - sd_x - .7, y = 40, label = "z = -1", color = "blue", vjust = -0.5) +
  annotate("text", x = mean_x + 2 * sd_x - .7, y = 40, label = "z = +2", color = "purple", vjust = -0.5) +
  annotate("text", x = mean_x - 2 * sd_x - .7, y = 40, label = "z = -2", color = "purple", vjust = -0.5) +

  # IQR annotations
  annotate("text", x = Q1, y = 45, label = "Q1", color = "orange", vjust = -0.5) +
  annotate("text", x = Q3, y = 45, label = "Q3", color = "orange", vjust = -0.5) +
  annotate("text", x = lower_fence, y = 30, label = "Lower Fence", color = "brown", angle = 90, vjust = -0.4) +
  annotate("text", x = upper_fence, y = 30, label = "Upper Fence", color = "brown", angle = 90, vjust = -0.4)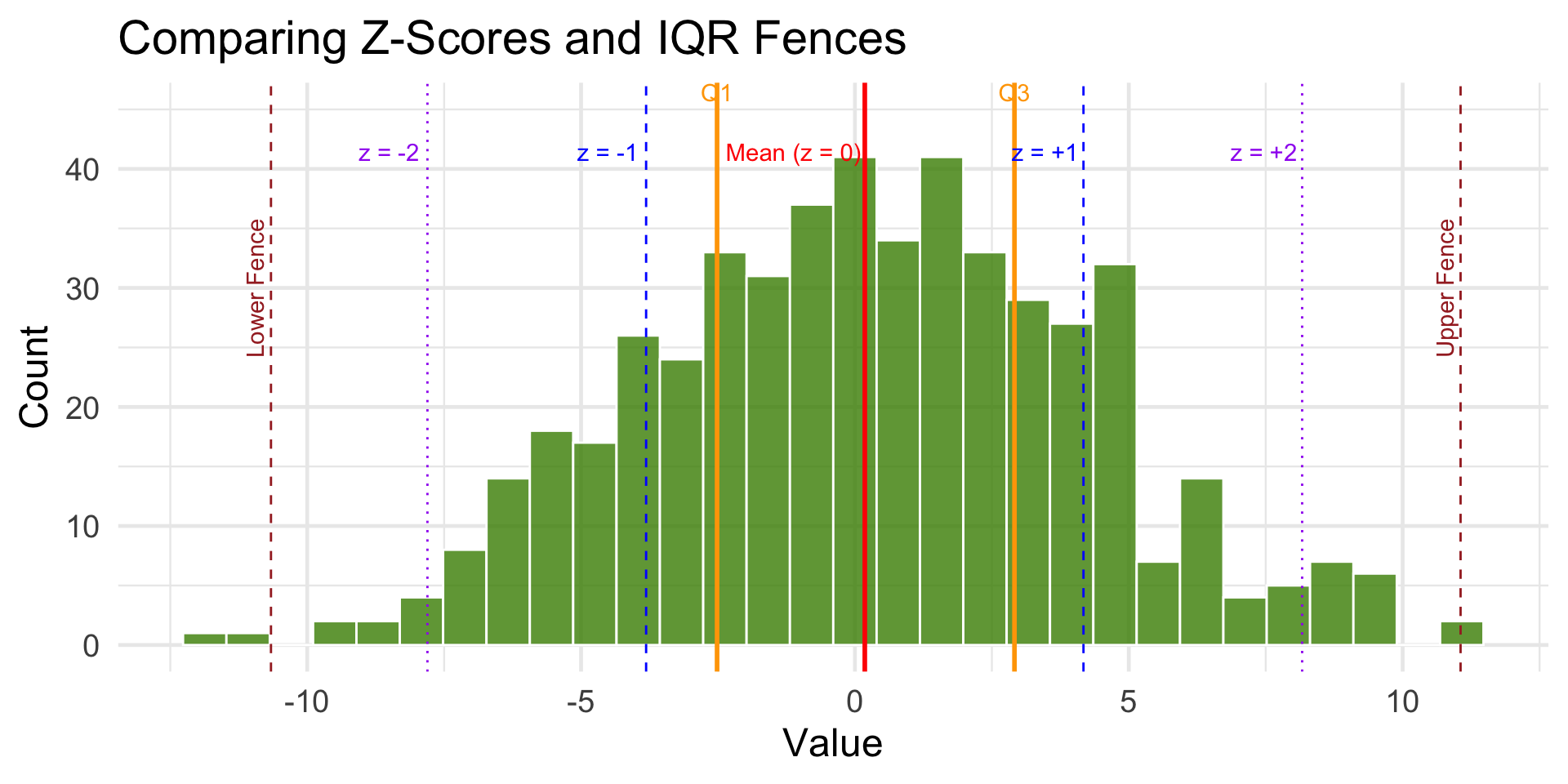

Summary of Outliers

Type	Formula	Purpose	Common Use
Mild Fence	Q1 - 1.5 × IQR Q3 + 1.5 × IQR	Detects mild outliers	Standard boxplots
Extreme Fence	Q1 - 3 × IQR Q3 + 3 × IQR	Detects extreme outliers	Detailed exploration
2 SD Threshold	Mean ± 2 × SD	Captures ~95% of normal data	Quality control, z-scores
3 SD Threshold	Mean ± 3 × SD	Flags rare deviations (~99.7%)	Detecting anomalies