Sampling and Uncertainty
Sarah Cassie Burnett
October 23, 2025
Sampling
- Sampling the act of selecting a subset of individuals, items, or data points from a larger population to estimate characteristics or metrics of the entire population
- Versus a census, which involves gathering information on every individual in the population
- Why would you want to use a sample?
Target Population
In data analysis, we are usually interested in saying something about a Target Population.
- How many US college students check social media during their classes?
- Target population: US college students
- What is the average time students spend commuting to campus each day?
- Target population: College students who attend in-person classes
- What is the average number of fries in a small order at McDonald’s?
- Target population: all small fry orders at McDonald’s.
Sample
In many instances, we have a sample to talk about
We cannot talk to all college students
We cannot monitor all french fry orders
Parameters vs Statistics
- The parameter is the value of a calculation for the entire target population
- The statistic is what we calculate on our sample
- We calculate a statistic in order to say something about the parameter
Inference
- Inference—The act of “making a guess” about some unknown
- Statistical inference—Making a good guess about a population from a sample
- Causal inference—Did X cause Y?
Uncertainty
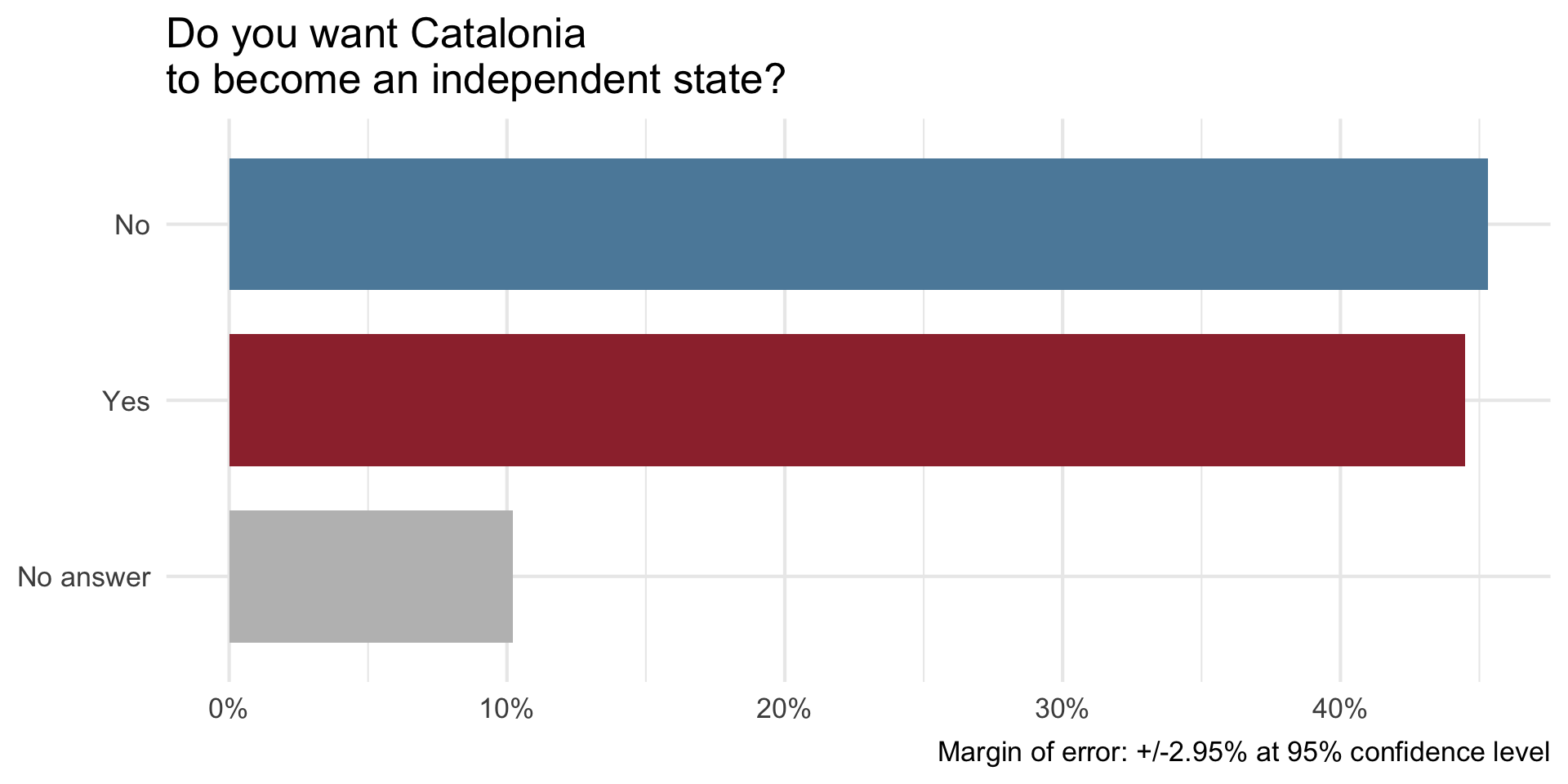
On December 19, 2014, the front page of Spanish national newspaper El País read “Catalan public opinion swings toward ‘no’ for independence, says survey”.1
The probability of the tiny difference between the ‘No’ and ‘Yes’ being just due to random chance is very high.1
Characterizing Uncertainty
- Even unbiased procedures do not get the “right” answer every time
- Estimates vary from sample to sample due to random chance
- Therefore we report our estimate and our uncertainty
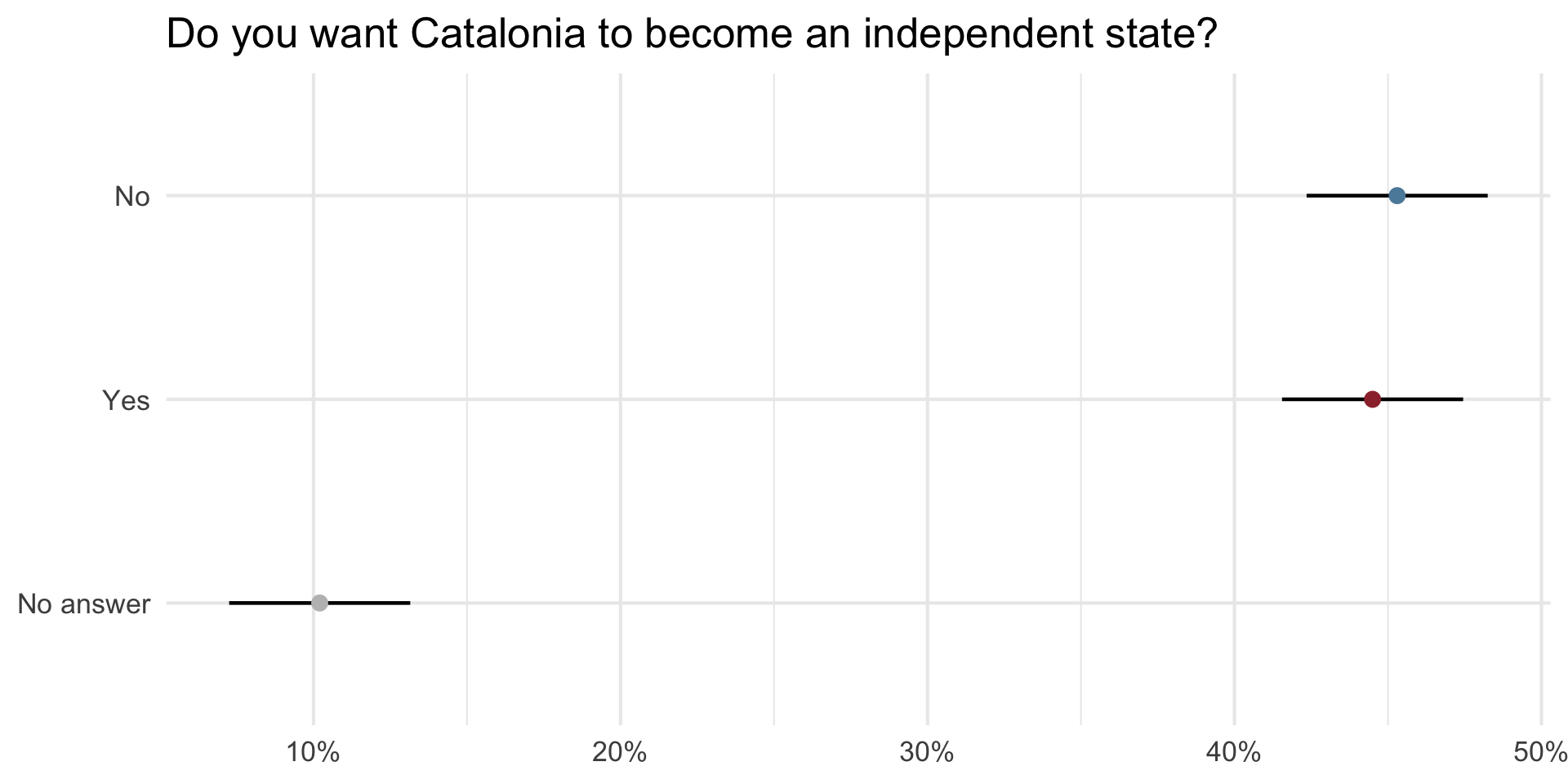
Solution: Create a Confidence Interval
- A plausible range of values for the population parameter is a confidence interval.
- 95% confidence interval is standard:
- We are 95% confident that the parameter value falls within the interval
Ways to Estimate
- Using math (via the Central Limit Theorem)
- Using simulation (bootstrapping)
With Math…
\[CI = \bar{x} \pm Z \left( \frac{\sigma}{\sqrt{n}} \right)\]
- \(\bar{x}\) is the sample mean,
- \(Z\) is the Z-score corresponding to the desired level of confidence
- \(\sigma\) is the population standard deviation, and
- \(n\) is the sample size
We rarely have the true \(\sigma\)…
This part here represents the standard error:
\[\left( \frac{\sigma}{\sqrt{n}} \right)\]
- Standard deviation of the sampling distribution
- Characterizes the spread of the sampling distribution
- The bigger this is the bigger the CIs are going to be
Common Z-values
| Confidence Level | Z-Value (±) |
|---|---|
| 80% | 1.28 |
| 90% | 1.645 |
| 95% | 1.96 |
| 99% | 2.576 |
Central Limit Theorem
Confidence Interval (CI)
\[CI = \bar{x} \pm Z \left( \frac{\sigma}{\sqrt{n}} \right)\]
- This way of doing things depends on the Central Limit Theorem
- As sample size gets bigger, the spread of the sampling distribution gets narrower
- The shape of the sampling distributions becomes more normally distributed
Estimating Uncertainty with Confidence Intervals
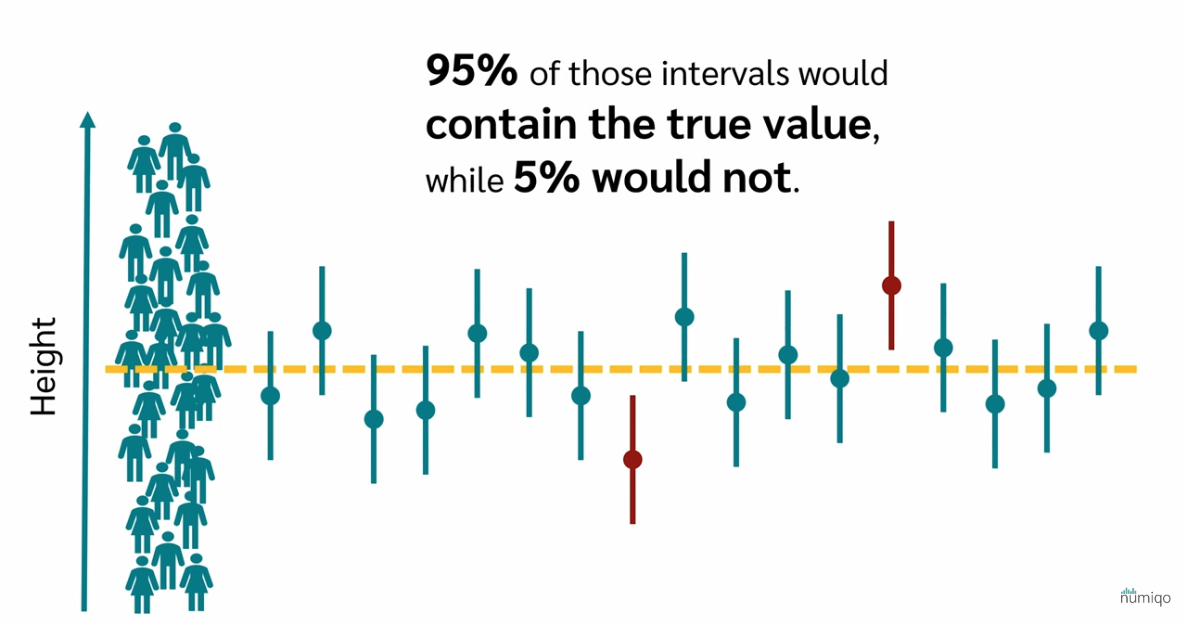
A confidence interval gives us a range of plausible values for a population parameter.
A 95% confidence interval means that if we repeated our sampling many times,
Conceptual Example: Student Screen Time
Suppose we survey 100 students about their average daily screen time (in hours).
- Sample mean = 6.2 hours
- Standard deviation = 1.5 hours
- Standard error = 1.5 / √100 = 0.15
The 95% confidence interval is:
\[ 6.2 \pm 1.96 \times 0.15 = (5.91, 6.49) \]
We are 95% confident that the true average daily screen time among all students is between 5.9 and 6.5 hours.
Confidence Interval
\[CI = \bar{x} \pm Z \left( \frac{\sigma}{\sqrt{n}} \right)\]
This is therefore a parametric method of calculating the CI. It depends on assumptions about the normality of the distribution — that we know the parameters \(\sigma\) and \(\bar{x}\).
Bootstrapping
- Use the data you have to approximate the sampling distribution
- Take many with-replacement resamples of size (n)
- Compute the statistic each time (mean/median/prop/etc.)
- Use the middle XX% of the bootstrap statistics for the CI (e.g., 95%)
- This is nonparametric—no normality assumption required
Bootstrap Process
- Take a bootstrap sample - a random sample taken with replacement from the original sample, of the same size as the original sample
- Calculate the bootstrap statistic - a statistic such as mean, median, proportion, slope, etc. computed on the bootstrap samples
- Repeat steps (1) and (2) many times to create a bootstrap distribution - a distribution of bootstrap statistics
- Calculate the bounds of the XX% confidence interval as the middle XX% of the bootstrap distribution (usually 95 percent confidence interval)
Russia
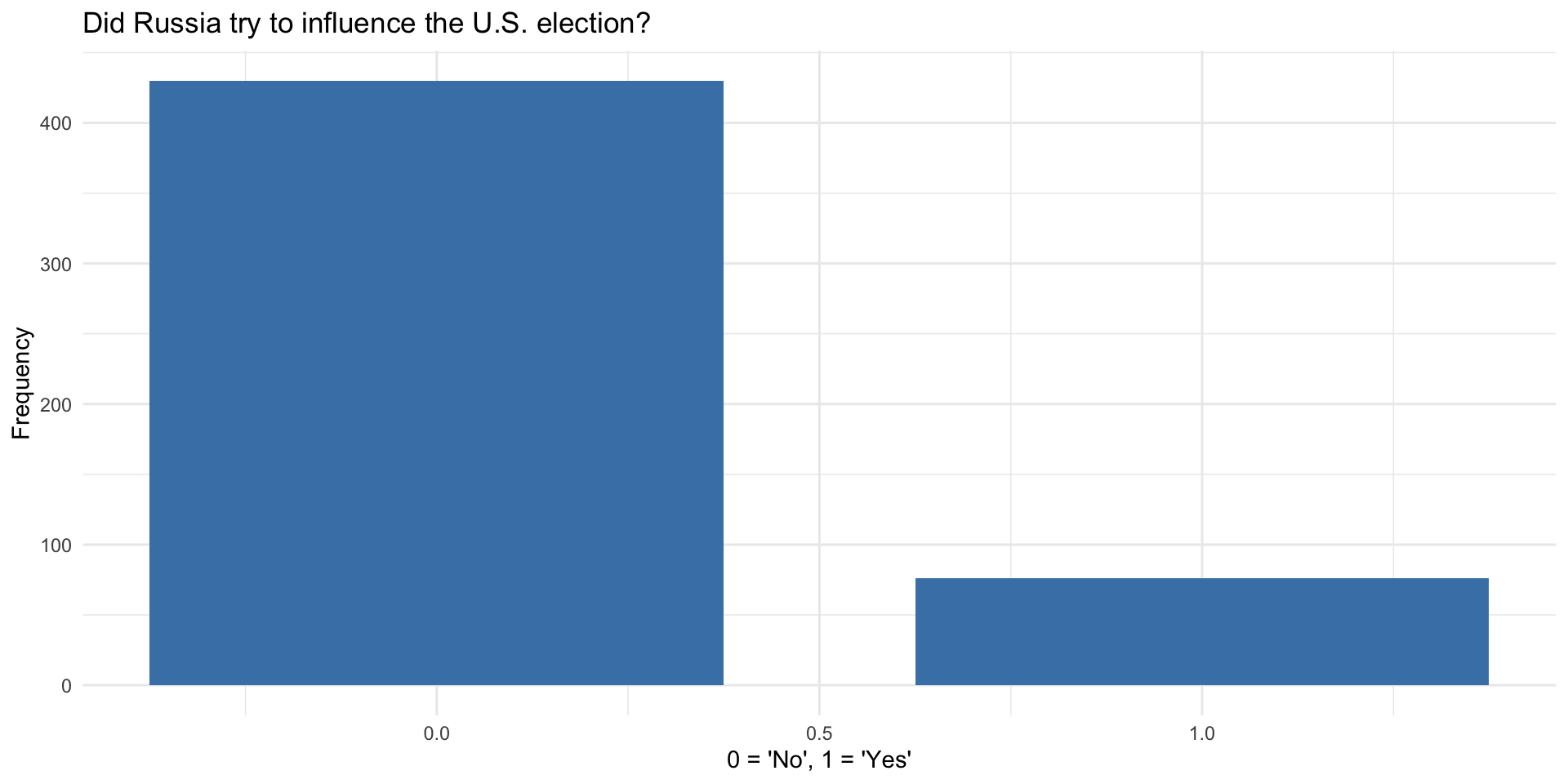
What Proportion of Russians believe their country interfered in the 2016 presidential elections in the US?
- Pew Research survey
- 506 subjects
- Data available in the
openintropackage
For this example, we will use data from the Open Intro package. Install that package before running this code chunk.
Let’s use mutate() to recode the qualitative variable as a numeric one…
Now let’s calculate the mean and standard deviation of the try_influence variable…
And finally let’s draw a bar plot…
Bootstrap with tidymodels
Install tidymodels before running this code chunk…
#install.packages("tidymodels")
library(tidymodels)
set.seed(66)
boot_dist <- russiaData |>
specify(response = try_influence) |> # specify the variable of interest
generate(reps = 10000, type = "bootstrap") |> # generate 10000 bootstrap samples
calculate(stat = "mean") # calculate the mean of each bootstrap sample
glimpse(boot_dist)Rows: 10,000
Columns: 2
$ replicate <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ stat <dbl> 0.1146245, 0.1442688, 0.1343874, 0.1877470, 0.1521739, 0.138…Calculate the mean of the bootstrap distribution (of the means of the individual draws)…
Calculate the confidence interval. A 95% confidence interval is bounded by the middle 95% of the bootstrap distribution.
Create upper and lower bounds for visualization.
Visualize with a histogram
ggplot(data = boot_dist, mapping = aes(x = stat)) +
geom_histogram(binwidth =.01, fill = "steelblue4") +
geom_vline(xintercept = c(lower_bound, upper_bound), color = "darkgrey", size = 1, linetype = "dashed") +
labs(title = "Bootstrap distribution of means",
subtitle = "and 95% confidence interval",
x = "Estimate",
y = "Frequency") +
theme_bw()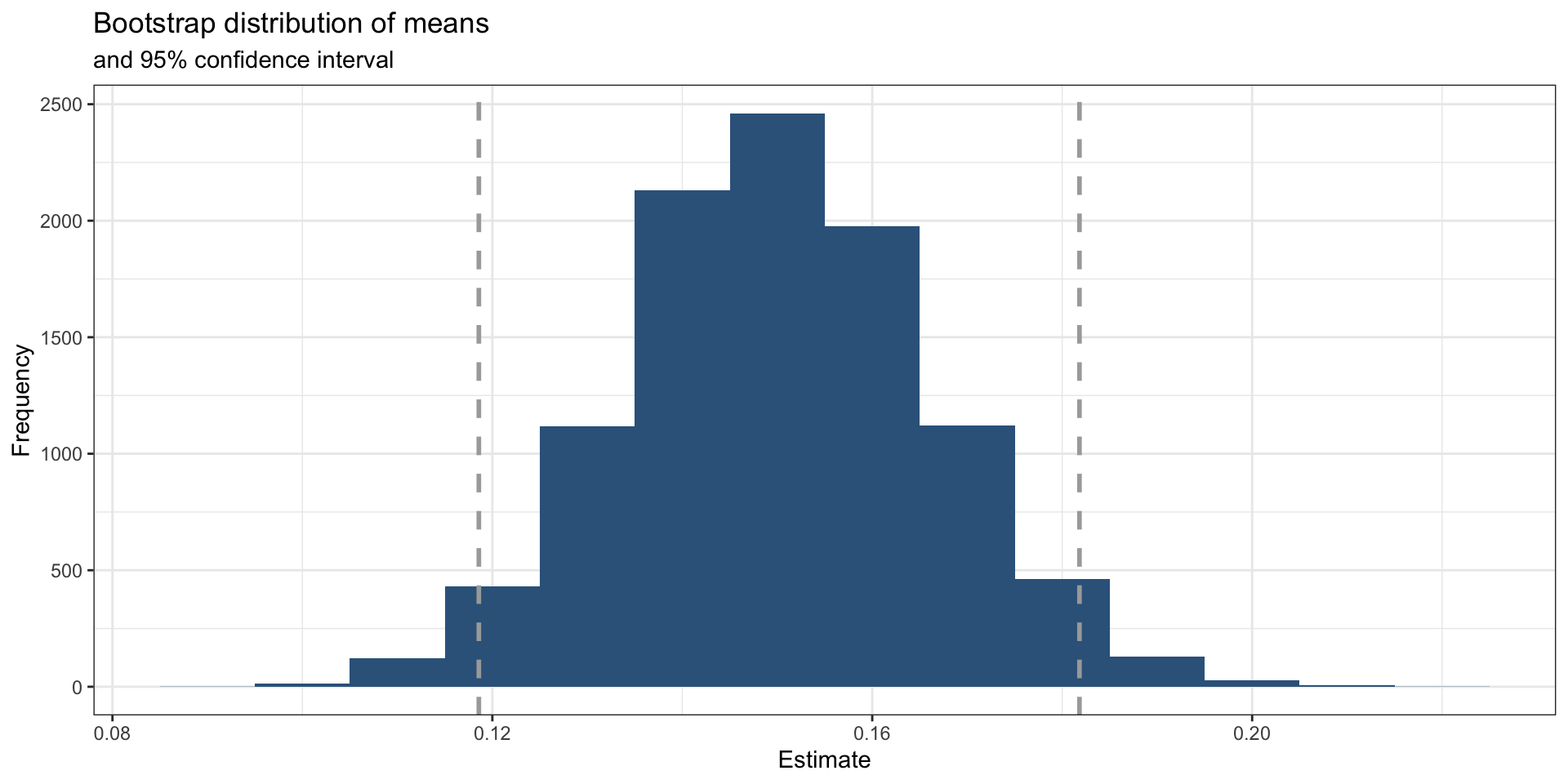
Or use the infer package
Or use the infer package
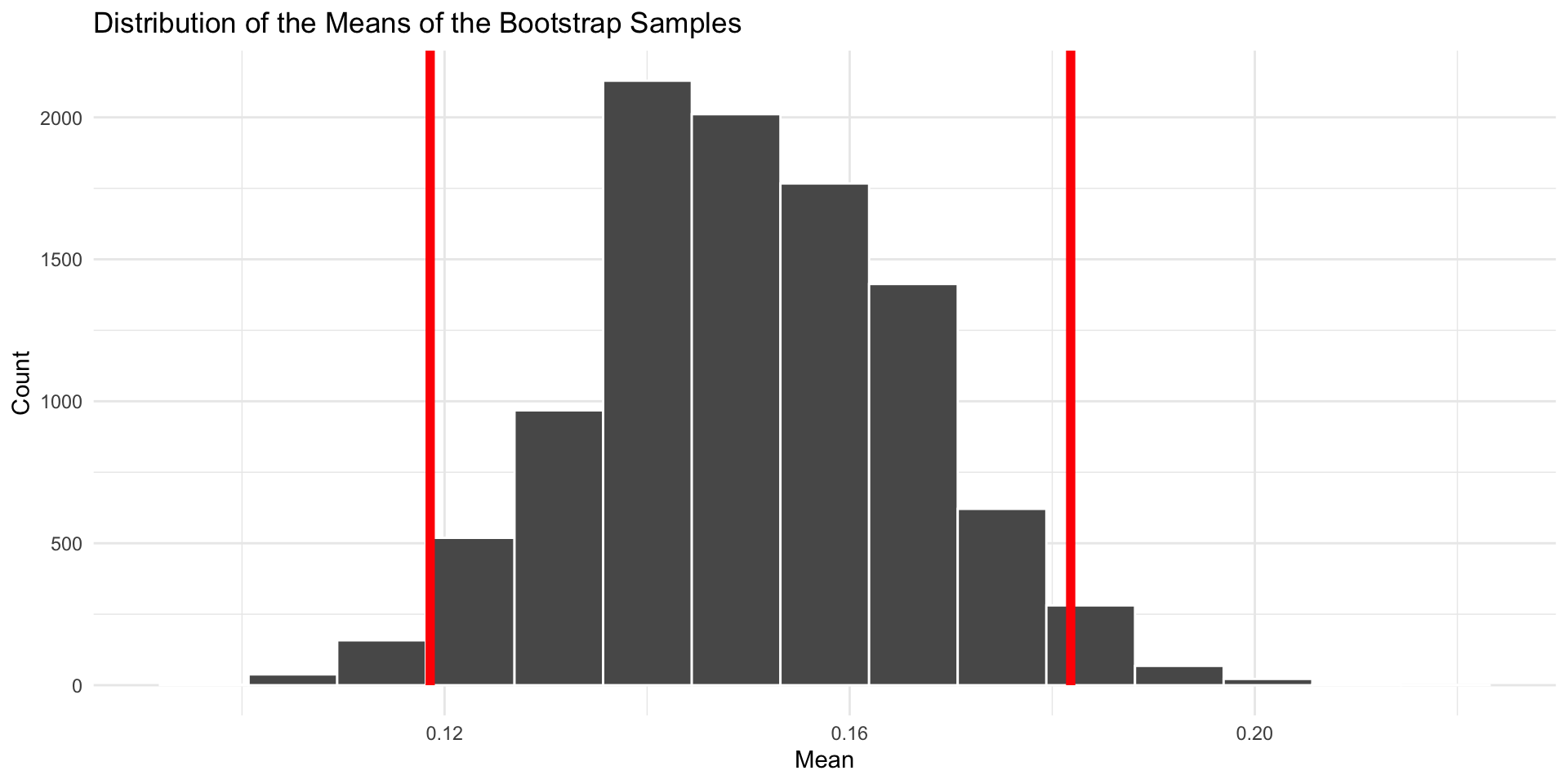
Or use the infer package
Interpret the confidence interval
The 95% confidence interval was calculated as (lower_bound, upper_bound). Which of the following is the correct interpretation of this interval?
(a) 95% of the time the percentage of Russian who believe that Russia interfered in the 2016 US elections is between lower_bound and upper_bound.
(b) 95% of all Russians believe that the chance Russia interfered in the 2016 US elections is between lower_bound and upper_bound.
(c) We are 95% confident that the proportion of Russians who believe that Russia interfered in the 2016 US election is between lower_bound and upper_bound.
(d) We are 95% confident that the proportion of Russians who supported interfering in the 2016 US elections is between lower_bound and upper_bound.
Interpret the confidence interval
The 95% confidence interval was calculated as (lower_bound, upper_bound). Which of the following is the correct interpretation of this interval?
(c) We are 95% confident that the proportion of Russians who believe that Russia interfered in the 2016 US election is between lower_bound and upper_bound.
Try it out!
Given that the mean of 0-1 encoded data is equal to the proportion, use the following formula to estimate the confidence interval based on the sample of 506 Russians,
03:00
We estimate the standard error using:
\[ SE = \sqrt{ \frac{ \hat{p}(1 - \hat{p}) }{n} } \]
Tips:
- To count rows:
nrows(your_data) - To access a column in a data frame:
your_data$col_name
Why did we do these simulations?
- They provide a foundation for statistical inference and for characterizing uncertainty in our estimates
- The best research designs will try to maximize or achieve good balance on bias vs precision